Trong đường tròn tâm M nói trên, ta có DE là dây, BC là đường kính nên DE < BC

Trong đường tròn tâm M nói trên, ta có DE là dây, BC là đường kính nên DE < BC
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC.
Cho tam giác ABC nhọn và có các đường cao BD, CE. Chứng minh:
a, Các điểm B, D, C, E cùng thuộc một đường tròn
b, BC > DE
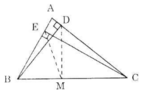
Cho tam giác ABC có ba góc nhọn, các đường cao BD, CE. Gọi M là trung điểm cạnh BC
a) Chứng minh rằng AE.AB=AF.AC
b) Chứng minh rằng DE=BC.cosA
c) Cho \(\widehat{BAC=60^0}\), Chứng minh tam giác MDE đều
Cho BC là dây cung cố ddingj của đường tròn (O;R) (BC # 2R) . A là điểm chuyển động trên cung lớn BC sao cho tam giác ABC nhọn. Các đường cao BD, CE của tam giác ABC cắt nhau tại H.
a, Chứng minh rằng : A, D, H, E cùng thuộc một đường tròn và AH > DE
b, K là trung điểm của BC
Chứng minh rằng: AH // OK
c, Xác định vị trí của điểm A để diện tích tam giác ABC lớn nhất
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A;AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H).
Chứng minh rằng:
DE tiếp xúc với đường tròn các đường kính BC
Cho tam giác ABC nhọn có góc A bằng 60 độ và có 2 đường cao BD và CE Chứng minh: BC bằng 2 DE
cho tam giác ABC nhọn, đường cao BD,CE cắt nhau ở H. DE cắt BC ở F, M là trung điểm của BC. chứng minh rằng FH vuông góc AM
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O. 3 đường cao AK, BD, CE cắt nhau tại H. Gọi I,J lần lượt là trung điểm của DE và BC. Chứng minh rằng OA // JI
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Ba đường cao BD;
CE và AF của tam giác ABC cắt nhau tại điểm H. Chứng minh rằng:
1) Góc DEC = Góc DBC.
2) CE.HC + BD.HB = BC2
3) Đường thẳng DE vuông góc OA