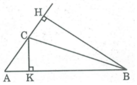
Ta có: S A B C = 1/2 AB.CK = 1/2 AC.BH
Suy ra: AB.CK = AC.BH ⇒ ![]()
Mà AB = 3AC (gt) ⇒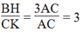
Vậy đường cao BH dài gấp 3 lần đường cao CK.

Ta có: S A B C = 1/2 AB.CK = 1/2 AC.BH
Suy ra: AB.CK = AC.BH ⇒ ![]()
Mà AB = 3AC (gt) ⇒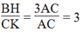
Vậy đường cao BH dài gấp 3 lần đường cao CK.
Cho tam giác ABC, AB=3AC. Tính tỉ số đường cao xuất phát từ B và C
Cho ΔABC biết AB = 3AC. Tỉ số hai đường cao xuất phát từ các đỉnh B và C là:
A. 3
B. 4
C. 5
D. 6
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ đỉnh B và C. Bài 2 Cho hình thang vuông ABCD (∠A = ∠D = 90°). Gọi H là điểm đối xứng với B qua AD, I là giao điểm của CH và AD. Chứng minh rằng ∠(AIB) = ∠(DIC)
Cho tam giác ABC có AB=12 cm, AC=16cm. Hai đường cao xuất phát từ đỉnh B và C là BH và CK . Biết BH=9cm. Tính CK.
A. 12cm
B. 15cm
C. 9cm
D. 8cm
cho tam giác ABC biết AB=AC. Kẻ đường cao BH và CK.
a) Viết công thức tính diện tích tam giác ABC theo độ dài đường cao BH VÀ CK.
b)tỉ số 2 đường chép xuất phát từ các đỉnh B cà C.
c)so sánh độ dài 2 đường cao BH VÀ CK.
Cho tam giác ABC. Tính tỉ số đường cao BB’, CC’ xuất phát từ đỉnh B, C
cho tam giác ABC;AB =3AC .tinh tỷ số đường cao xuất phát B và C
Cho tam giác ABC. Đường thẳng xuất phát từ đỉnh A cắt BC tại K và cắt đường trung tuyến BM tại I sao cho \(\frac{BI}{IM}\)= \(\frac{1}{2}\). Tính tỉ số diện tích tam giác ABK và tam giác ABC .
Cho tam giác ABC có đường cao kẻ từ A, đường trung tuyến xuất phát từ B và đường phân giác kẻ từ đỉnh C đồng qui. Gọi a, b, c lần lượt là độ dài 3 cạnh BC, AC, AB. Chứng minh (a + b)(a2 + b2 - c2) = 2a2b