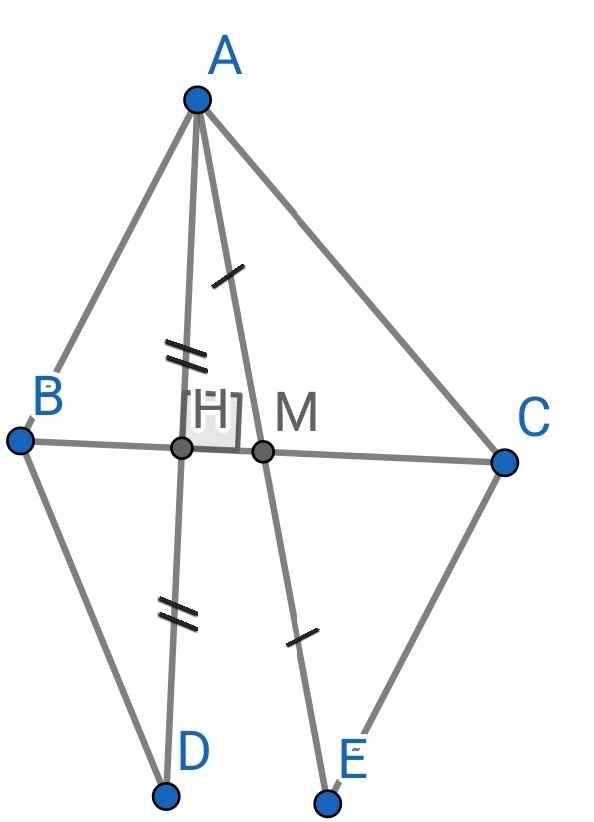
a/
Xét tg MAB và tg MEC có
MB=MC (gt); MA=ME (gt)
\(\widehat{AMB}=\widehat{EMC}\) (góc đối đỉnh)
=> tg MAB = tg MEC (c.g.c)
b/
Ta có tg MAB = tg MEC (cmt) \(\Rightarrow\widehat{BAM}=\widehat{CEM}\)
Hai góc trên ở vị trí so le trong => AB//CE
c/
Xét tg vuông ABH và tg vuông DBH có
HA=HD (gt); BH chung => tg ABH = tg DBH (hai tg vuông có 2 cạnh góc vuông bằng nhau) => AB=BD(1)
Ta có tg MAB = tg MEC (cmt) => AB=CE (2)
Từ (1) và (2) => BD=CE
 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Xét ∆MAB và ∆MEC có:
BM = MC (cmt)
∠AMB = ∠EMC (đối đỉnh)
AM = ME (gt)
⇒ ∆MAB = ∆MEC (c-g-c)
b) Do ∆MAB = ∆MEC (cmt)
⇒ ∠MAB = ∠MEC (hai góc tương ứng)
Mà ∠MAB và ∠MEC là hai góc so le trong)
AB // CE
c) Xét hai tam giác vuông: ∆AHB và ∆DHB có:
BH là cạnh chung
AH = HD (gt)
⇒ ∆AHB = ∆DHB (hai cạnh góc vuông)
⇒ AB = BD (hai cạnh tương ứng)
Do ∆MAB = ∆MEC (cmt)
⇒ AB = CE (hai cạnh tương ứng)
Mà AB = BD (cmt)
⇒ BD = CE















