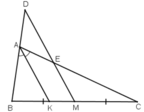
AK là đường phân giác của tam giác ABC nên:
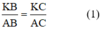
Ta có: MD // AK
⇒ ΔABK 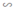 ΔDBM và ΔECM
ΔDBM và ΔECM 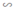 ΔACK
ΔACK
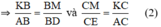
Từ (1) và (2) ta có: 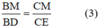
Do BM = CM (giả thiết) nên từ (3) suy ra: BD = CE.

AK là đường phân giác của tam giác ABC nên:
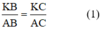
Ta có: MD // AK
⇒ ΔABK 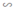 ΔDBM và ΔECM
ΔDBM và ΔECM 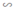 ΔACK
ΔACK
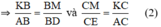
Từ (1) và (2) ta có: 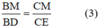
Do BM = CM (giả thiết) nên từ (3) suy ra: BD = CE.
Giải giúp mình bài toán này với, mình xin cảm ơn trước : Cho tam giác ABC (AB < AC). Tia phân giác của góc A cắt BC ở K. Qua trung điểm M của BC kẻ một tia song song với KA cắt đường thẳng AB ở D, cắt AC ở E. Chứng minh BD = CE.
cho tam giác ABC (AB<AC) .Tia phân giác của góc A cắt BC ở K.Qua trung điểm M của BC kẻ 1 tia song song với KA cắt đường thẳng AB ở D,cắt AC ở E .Chúng minh BD=CE
Cho tam giác ABC. Trên tia đối của BC lấy điểm D, trên tia đối của CB lấy điểm E sao cho BD=BC=CE. Qua D kẻ đường thẳng song song ới AB cắt AC ở H. Qua E kẻ đường thẳng song song với AC cắt AB ở K,chúng cắt nhau ở I.
a) Tứ giác BHKC là hình gì? Vì sao ?
b) Tia IA cắt BC ở M. Chứng minh MB=MC
c) Tìm điều kiện của tam giác ABC để tứ giác DHKE là hình thang cân
1. Cho tam giác ABC, điểm D thuộc cạnh BC. Qua D kẻ các đường thẳng song song AB và AC chúng cắt AB,AC theo thứ tự ở E và F. Chứng minh hệ thức: AE/AB+AF/AC=1
2. Cho tam giác ABC, 1 đường thẳng song song với BC cắt các cạnh AB, AC theo thứ tự ở D và E. Qua C kẻ đường thẳng song song với EB cắt AB ở F. Chứng minh hệ thức AB2=AD*AF
3.Cho tam giác ABC( AB<AC) đường phân giác AD. Qua trung điểm M của BC kẻ đường thẳng song song với AD cắt AC và AB theo thứ tự ở E và K. Chứng minh rằng:
a. AE=AK
b. DK=CE
cho tam giác ABC có góc A tù, BD là tia phân giác của góc B (D ∈ AC)
Qua trung điểm M của AC kẻ đường thẳng song song với BD, đường thẳng này lần lượt cắt đoạn thẳng BC ở N và cắt tia AB ở P.
a, BNP là tam giác cân ( đã cm)
b, Cmr AB=NC-NB
c, cho AB=a và BC=2a, tính tỉ số diện tích của 2 tam giác ABC và ANC
Bài 6: Cho hình thang ABCD có hai đáy là AB và CD. Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E và F.
a) Chứng minh ED/AD + BF/BC = 1
b) Các đường chéo của hình thang cắt nhau tại O. Chứng minh OA.OD = OB.OC.
Bài 7: Cho tam giác ABC nhọn, M là trung điểm của BC, E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D, cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC ở F.
a) Chứng minh CF = DK
b) Gọi H là trực tâm của tam giác ABC. Đường thẳng qua H vuông góc với MH cắt AB và AC theo thứ tự ở I và K’. Qua C kẻ đường thẳng song song với IK’, cắt AH và AB theo thứ tự ở N và P. Chứng minh NC = NP và HI = HK’.
Bài 8: Cho tam giác ABC, điểm M bất kì trên cạnh AB. Qua M kẻ đường thẳng song song với BC cắt AC ở N biết AM = 11 cm, MB = 8 cm, AC = 38 cm. Tính độ dài các đoạn thẳng AN, NC.
Bài 9: Cho góc xAy, trên tia Ax lấy hai điểm D và E, trên tia Ay lấy hai điểm F và G sao cho FD song song với EG. Đường thẳng qua G song song với FE cắt tia Ax tại H. Chứng minh AE 2 = AD.AH.
Bài 10: Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ quá F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG.
Cho ΔABC. Trên tia đối của tia BC lấy D, trên tia đối của tia CB lấy E sao cho BD=BC=CE. Qua D kẽ đường thẳng song song với AB và cắt AC ở H. Que E kẻ đường thẳng song song với AC và cắt AB ở K, chúng cắt nhau ở I'
a/ Tứ giác BHCK là hình gì? Vì sao?
b/ Tia IA cắt BC ở M. Chứng minh MB=MC
c/ Tìm điều kiện của ΔABC để tứ giác DHKE là h.t.cân
Cho tam giác ABC. Lấy các điểm D,E theo thứ tự thuộc tia đối của các tia BA, CA sao cho BD=CE=BC. Gọi O là giao điểm của BE và CD. Qua O vẽ đường thẳng song song với tia phân giác của góc A, đường thẳng này cắt AC ở K. Chứng minh rằng AB=CK
Cho tam giác ABC. M là trung điểm của BC, lấy điểm E thuộc MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D và cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC tại F. Chứng minh CF= DK