Question

cho tam giác abc , a=30, b=45, ab=12. tính ac,bc

Answer 1

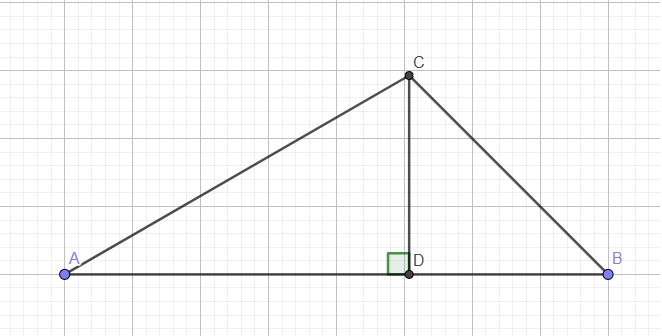
Hạ CD vuông góc AB

Trong tam giác vuông ACD:

\(cotA=\dfrac{AD}{CD}\)

Trong tam giác vuông BCD:

\(cotB=\dfrac{BD}{CD}\)

\(\Rightarrow cotA+cotB=\dfrac{AD}{CD}+\dfrac{BD}{CD}=\dfrac{AD+BD}{CD}=\dfrac{AB}{CD}\)

\(\Rightarrow CD=\dfrac{AB}{cotA+cotB}\)

Trong tam giác vuông ACD:

\(sinA=\dfrac{CD}{AC}\)

\(\Rightarrow AC=\dfrac{CD}{sinA}=\dfrac{AB}{sinA.\left(cotA+cotB\right)}=\dfrac{12}{sin30^0.\left(cot30^0+cot45^0\right)}=12\sqrt{3}-12\)

Trong tam giác vuông BCD:

\(sinB=\dfrac{CD}{BC}\)

\(\Rightarrow BC=\dfrac{CD}{sinB}=\dfrac{AB}{sinB\left(cotA+cotB\right)}=\dfrac{12}{sin45^0\left(cot30^0+cot45^0\right)}=6\sqrt{6}-6\sqrt{2}\)

Answer 2