Chọn A.
• Trước hết ta chứng minh được, với hai số ![]()
• Theo giả thiết
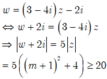
Chọn A.
• Trước hết ta chứng minh được, với hai số ![]()
• Theo giả thiết
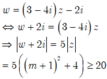
Cho số phức z thỏa mãn |z| = 1 m 2 + 2m, trong đó m là số thực dương tùy ý. Biết rằng với mỗi m, tập hợp các điểm biểu diễn số phức w = (2i+1)(i+ z ¯ )-5+3i là một đường tròn bán kính r. Tìm giá trị nhỏ nhất của r
A . 3 2
B . 2 3
C . 3 5
D . 5 3
Cho số phức z thỏa mãn |z|=1. Biết tập hợp các điểm biểu diễn số phức w = (3 - 4i)z -1 + 2i là đường tròn tâm I, bán kính R. Tìm tọa độ tâm I và bán kính R của đường tròn đó.
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn |z| = 1. Biết tập hợp các điểm biểu diễn số phức w = (3 - 4i)z -1 + 2i là đường tròn tâm I, bán kính R. Tìm tọa đọ tâm I và bán kính R của đường tròn đó
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z - 1 = 5 . Biết tập hợp các điểm biểu diễn số phức w xác định bởi w = ( 2 + 3 i ) . z ¯ + 3 + 4 i là một đường tròn bán kính R. Tính R
A. R= 5 17
B. R= 5 10
C. R= 5 5
D. R= 5 13
Cho số phức z thỏa mãn z - 1 = 5 Biết tập hợp các điểm biểu diễn số phức w xác định bởi w = 2 + 3 i . z + 3 + 4 i là một đường tròn bán kính R. Tính R
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z = 2 Biết rằng tập hợp các điểm biểu diễn số phức w=3-2i+(2-i)z là một đường tròn. Bán kính R của đường tròn đó bằng bao nhiêu?
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z = 2 Biết rằng tập hợp các điểm biểu diễn số phức w=3-2i+(2-i)z là một đường tròn, bán kính R của đường tròn đó bằng
A. 7
B. 20
C. 2 5
D. 7
Cho số phức ![]() thỏa mãn |z-2i|=m^2+4m+6, với m là số thực. Biết rằng tập hợp các điểm biểu diễn của số phức w=(4-3i)z+2i là đường tròn. Bán kính của đường tròn đó có giá trị nhỏ nhất bằng
thỏa mãn |z-2i|=m^2+4m+6, với m là số thực. Biết rằng tập hợp các điểm biểu diễn của số phức w=(4-3i)z+2i là đường tròn. Bán kính của đường tròn đó có giá trị nhỏ nhất bằng
A.![]() .
.
B.2.
C.10.
D.![]() .
.
Cho các số phức z thỏa mãn z + 1 = 2 . Biết rằng tập hợp các điểm biểu diễn các số phức w = ( 1 + i 8 ) z + i là một đường tròn. Bán kính r của đường tròn đó là
![]()
![]()
![]()
![]()