Đáp án A.
Ta có ![]()
![]()
![]()
Lấy môđun hai vế, ta được ![]()
![]()
Đặt ![]() khi đó (*)
khi đó (*) ![]()
![]()
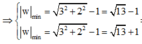
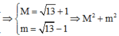
![]()
Đáp án A.
Ta có ![]()
![]()
![]()
Lấy môđun hai vế, ta được ![]()
![]()
Đặt ![]() khi đó (*)
khi đó (*) ![]()
![]()
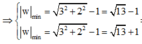
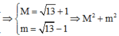
![]()
Cho số phức z thỏa mãn |z - 3 - 4i| = 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = | z + 2 | 2 - | z - i | 2 . Tính môđun của số phức w = M + mi ?
A. |w| = 2315
B. |w| = 1258
C. |w| = 3 137
D. |w| = 2 309
Cho số phức z thỏa mãn z - 2 + 3 i = 5 . Gọi m, M lần lượt là giá trị nhỏ nhất và lớn nhất của biểu thức P = z + i 2 - z - 2 2 . Tính A= m + M.
A. A = -3
B. A = -2
C. A = 5
D. A = 10
Cho số phức z thỏa mãn |z - 3 - 4i| = 5 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = | z + 2 | 2 - | z - 1 | 2 . Tính mô đun của số phức ω = M + mi
A. | ω | = 1258
B. | ω | = 3 137
C. | ω | = 2 134
D. | ω | = 2 309
Có bao nhiêu giá trị nguyên của m để có đúng 2 số phức z thỏa mãn z - ( m - 1 ) + i = 8 và z - 1 + i = z - 2 + 3 i .
A. 130
B. 66
C. 65
D. 131
Cho số phức z thỏa mãn |z + 2 - i| + |z - 5 + 6i| = 7 2 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = |z - 1 + 2i|. Tổng M + m là:
A. 2.
B. 3 2
C. 4 2
D. 7 2
Cho số phức z thỏa mãn 5 z - i = z + 1 - 3 i + 3 z - 1 + i .
Tìm giá trị lớn nhất M của z - 2 + 3 i
A. M= 10 3
B. M= 1 + 3
C. M= 4 5
D. M= 9
Cho số phức z thỏa mãn | ( z + 2 ) i + 1 | + | ( z ¯ - 2 ) i - 1 | = 10 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z|. Tính tổng S=M+m.
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn z - 2 + i + z + 1 - i = 13 Tìm giá trị nhỏ nhất m của biểu thức z + 2 - i
![]()
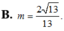

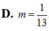
Cho số phức z thỏa mãn (2-i)z = (2+i)(1-3i). Gọi M là điểm biểu diễn của z. Khi đó tọa độ điểm M là.
A. M(3;1)
B. M(3;-1)
C. M(1;3)
D. M(1;-3)