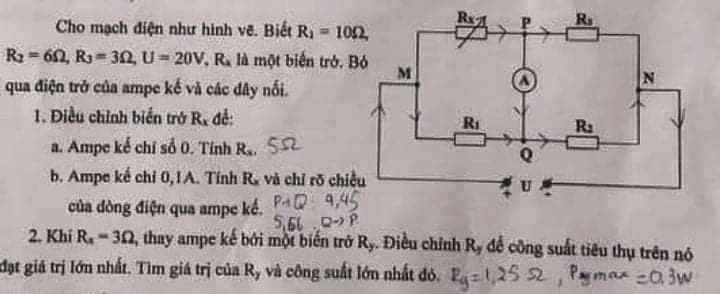
\(R1ntR2\Rightarrow P2=U2.I2=I2^2R2=Im^2.R2\)
\(\Rightarrow P2=\left(\dfrac{Um}{Rtd}\right)^2.R2=\left(\dfrac{12}{R1+R2}\right)^2.R2\)
\(\Rightarrow P2=\dfrac{12^2.R2}{\left(R1+R2\right)^2}=\dfrac{144R2}{\left(6+R2\right)^2}=\dfrac{144}{\dfrac{\left(6+R2\right)^2}{\sqrt{R2}^2}}=\dfrac{144}{\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2}\)
\(\Rightarrow\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2\ge\left(2\sqrt{6}\right)^2\ge24\left(AM-GM\right)\)
\(\Rightarrow P2=\dfrac{144}{\left(\dfrac{6}{\sqrt{R2}}+\sqrt{R2}\right)^2}\le\dfrac{144}{24}\le6W\Rightarrow P2max=6W\)
\(dấu\) \("="\) \(xảy\) \(ra\Leftrightarrow\dfrac{6}{\sqrt{R2}}=\sqrt{R2}\Leftrightarrow R2=6\Omega\)