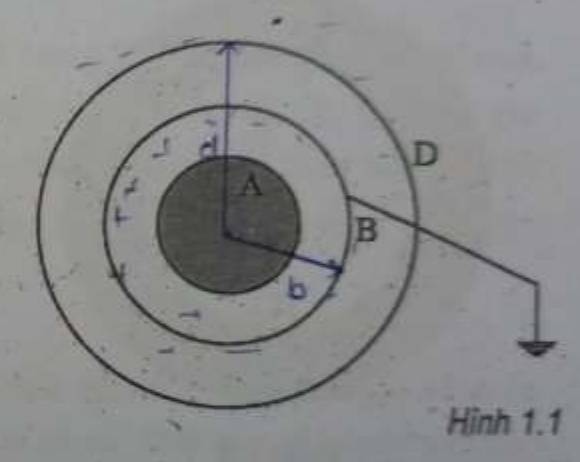
Cho quả cầu đặc, dẫn điện \(A\) và hai vỏ cầu dẫn điện \(B,D\) đặt đồng tâm với nhau. Vỏ cầu \(B\) nối với đất và đặt giữa \(A,D\). Quả cầu \(A\) mang điện tích \(+Q\), vỏ cầu \(D\) mang điện tích \(-Q.\) Biết bán kính của quả cầu \(A\), các vỏ cầu \(B,D\) lần lượt là \(a,b,d.\)
1. Tính điện tích các mặt trong, ngoài của \(D.\)
2. Tính hiệu điện thế giữa \(A\) và \(D\).
3. Tính hiệu điện thế giữa \(A\) và đất.
Để giải bài toán này, ta cần thực hiện các bước sau:
1. Tính điện tích các mặt trong và ngoài của \( D \).
2. Tính hiệu điện thế giữa \( A \) và \( D \).
3. Tính hiệu điện thế giữa \( A \) và đất.
Gọi:
- \( Q_A = Q \): Điện tích trên quả cầu \( A \)
- \( Q_D = -Q \): Điện tích trên vỏ cầu \( D \)
- \( a \): Bán kính của quả cầu \( A \)
- \( b \): Bán kính của mặt trong vỏ cầu \( B \)
- \( d \): Bán kính của mặt ngoài vỏ cầu \( D \)
1. Tính điện tích các mặt trong và ngoài của \( D \)
Vì vỏ cầu \( D \) là chất dẫn điện, điện tích \( -Q \) trên \( D \) sẽ phân bố như sau:
- Điện tích trên mặt trong của \( D \) sẽ là \( -Q \) để cân bằng với điện tích \( +Q \) trên \( A \).
- Điện tích trên mặt ngoài của \( D \) sẽ là \( +Q \) để đảm bảo tổng điện tích trên \( D \) là \( -Q \).
Do đó, mật độ điện tích mặt là:
- Mặt trong của \( D \):
\[ \sigma_{\text{trong}} = \frac{-Q}{4 \pi b^2} \]
- Mặt ngoài của \( D \):
\[ \sigma_{\text{ngoài}} = \frac{+Q}{4 \pi d^2} \]
2. Tính hiệu điện thế giữa \( A \) và \( D \)
Hiệu điện thế \( V \) tại khoảng cách \( r \) từ một quả cầu có bán kính \( a \) và điện tích \( Q \) được cho bởi:
\[ V(r) = \frac{Q}{4 \pi \epsilon_0 r} \]
Vì vậy, hiệu điện thế giữa \( A \) và mặt trong của \( D \) (ở khoảng cách \( b \)) là:
\[ V_{A} - V_{D_{\text{trong}}} = \frac{Q}{4 \pi \epsilon_0 a} - \frac{Q}{4 \pi \epsilon_0 b} \]
3. Tính hiệu điện thế giữa \( A \) và đất
Vì vỏ cầu \( B \) được nối đất, hiệu điện thế của nó bằng không. Do đó, hiệu điện thế giữa \( A \) và đất đơn giản là hiệu điện thế tại \( A \) trừ đi hiệu điện thế tại \( B \) (bằng không):
\[ V_{A} - V_{\text{đất}} = V_{A} - 0 = V_{A} = \frac{Q}{4 \pi \epsilon_0 a} \]
Vậy, các kết quả cuối cùng là:
1. Điện tích mặt:
- Mặt trong của \( D \): \(\sigma_{\text{trong}} = \frac{-Q}{4 \pi b^2}\)
- Mặt ngoài của \( D \): \(\sigma_{\text{ngoài}} = \frac{+Q}{4 \pi d^2}\)
2. Hiệu điện thế giữa \( A \) và \( D \):
\[ V_{A} - V_{D_{\text{trong}}} = \frac{Q}{4 \pi \epsilon_0} \left( \frac{1}{a} - \frac{1}{b} \right) \]
3. Hiệu điện thế giữa \( A \) và đất:
\[ V_{A} - V_{\text{đất}} = \frac{Q}{4 \pi \epsilon_0 a} \]
Chúc bạn học tốt nha!




