Đáp án `+` Giải thích các bước giải:
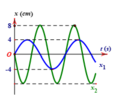
a. Tại `t = 0`: `x = 10cos(-pi/6) = 5sqrt{3} (cm) = (Asqrt{3})/2 `
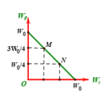
Tại `W_d = W_t` `=>` `W_t = 1/2 W = 1/2 kx^2 = 1/2 . 1/2 kA^2`
Suy ra: `x = +- A/sqrt{2} (cm)`
`\varphi < 0` `=>` Vật chuyển động theo chiều dương
Chu kì của vật là:
`T = (2pi)/omega = (2pi)/(4pi) = 0,5 (s)`
`t = (T/4 - T/6) + (T/4 - T/8) = (5T)/24 = (5.0,5)/24 = 5/48 (s)`
b. `W_t = 3W_d => x = +- sqrt{n/(n+1)} A = +- sqrt{3/(3+1)} A = +- (sqrt{3}A)/2`
`W_d` đang giảm `=>` Vật chuyển động về vị trí biên
Ban đầu, vật cũng ở vị trí có `W_t = 3W_d`, trong 1 chu kì có 4 lần như vậy
Thời gian cần tìm là:
`t' = (T/4 - T/6) + T/4 + T/6 = T/2 = (0,5)/2 = 0,25 (s)`.