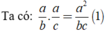
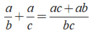
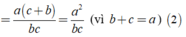
Từ (1), (2) ta có:
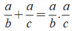 với b + c = a (a, b, c ∈ Z, b ≠ 0, c ≠ 0)
với b + c = a (a, b, c ∈ Z, b ≠ 0, c ≠ 0)
Nếu a = 8, b = -3 thì c = a - b = 8 - (-3) = 11
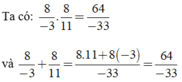
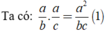
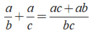
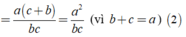
Từ (1), (2) ta có:
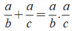 với b + c = a (a, b, c ∈ Z, b ≠ 0, c ≠ 0)
với b + c = a (a, b, c ∈ Z, b ≠ 0, c ≠ 0)
Nếu a = 8, b = -3 thì c = a - b = 8 - (-3) = 11
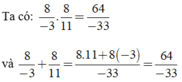
Cho phân số a/b và phân số a/c có b+c=a (a,b,c thuộc Z, b khác 0, c khác 0).
Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng. Thử lại với a=8, b=-3
Cho phân số a/b và phân số a/c có b+c=a (a,b,c thuộc Z, b khác 0, c khác 0).
Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng. Thử lại với a=8, b-3.
Cho phân số a/b và phân số a/c có b+c=a (a,b,c thuộc Z, b khác 0, c khác 0).
Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng. Thử lại với a=8, b-3.
cho phân số a/b và phân số a/c có b+c=a(a,b,c thuộc Z, b khác 0 , c khác 0 )
Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng . Thử lại với a=8,b= -3
cho phân số a/b và phân số a/c có b+c=a(a,b,c thuộc Z, b khác 0 , c khác 0 )
Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng . Thử lại với a=8,b= -3
Câu hỏi tương tự Đọc thêm
Toán lớp 6
Cho phân số \(\frac{a}{b}\)và phân số \(\frac{a}{c}\)có b+c=a (a,b,c\(\in\)Z, b\(\ne\)0, c\(\ne\)0).
Chứng tỏ rằng tích của hai phân số này bằng tổng của chúng. Thử lại với a=8, b=-3.
Cho phân số \(\frac{A}{B}\) và phân số \(\frac{a}{c}\) có b + c = a (a,b,c thuộc Z, b khác 0, c khác 0).
Chứng tỏ rằng tích của 2 phân số nay bằng tôngr của chúng. Thử lại với a=8, b=3.
Cho 2 phân só a/b và a/c có a+b=a(a,b,c thuộc Z, b,c Khác 0). Chứng tỏ rằng tích của 2 phân số này bằng tổng của chúng.
cho phân số \(\frac{a}{b}\)và \(\frac{c}{d}\)có b+c=a
(a,b,c thuộc Z ; b khác 0; c khác 0)
chứng tỏ rằng tích của hân số này = tổng của chúng
thử lại với a=8
b=-3