a: 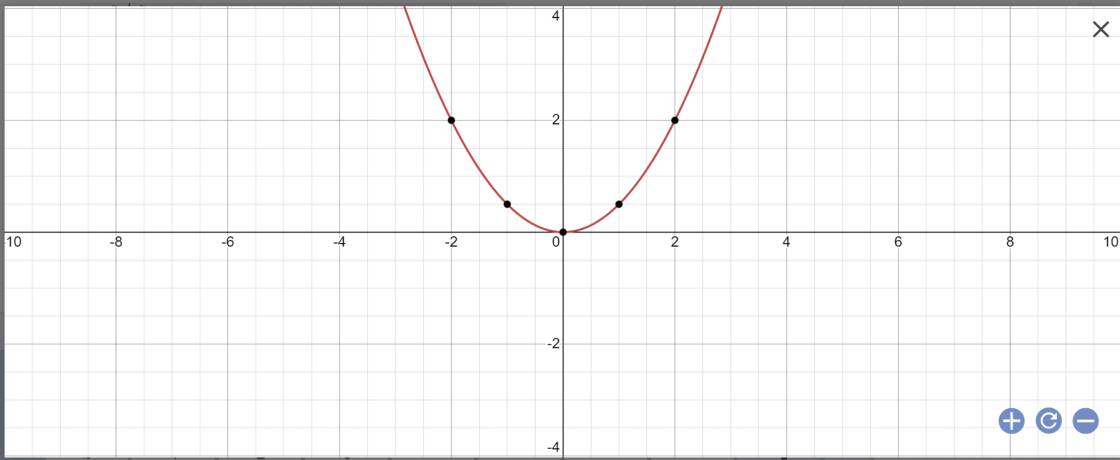
b: Khi x=-6 thì y=1/2*(-6)^2=18
=>M ko thuộc (P)
Khi x=căn 6 thì y=1/2*6=3
=>N thuộc (P)
c: PTHĐGĐ là;
1/2x^2-mx-3=0
a*c<0
=>(P) luôn cắt (d) tại hai điểm phân biệt
a: 
b: Khi x=-6 thì y=1/2*(-6)^2=18
=>M ko thuộc (P)
Khi x=căn 6 thì y=1/2*6=3
=>N thuộc (P)
c: PTHĐGĐ là;
1/2x^2-mx-3=0
a*c<0
=>(P) luôn cắt (d) tại hai điểm phân biệt
Cho parabol (P): y=1/2 x2 và đường thẳng (d): y=-mx+3(m là tham số)
a)Các điểm M(-6;-8) N(√6;3) có thuộc parabol (P) hay không?vì sao?
b)Chứng minh rằng với mọi giá trị của m đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt
Bài 5. (1 điểm) Cho parabol (P): y = −𝑥 ^2 và đường thẳng (d): y = mx − 1.
1. Chứng minh với mọi giá trị của m đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B.
2. Gọi 𝑥1 , 𝑥2 là hai hoành độ của A, B. Tìm m sao cho 𝑥1 ^3 + 𝑥2^ 3 = − 4.
Cho parabol (P) y=-x^2 và đường thẳng (d) y=mx-1
a) Với mọi giá trị của m, đường thẳng (d) luôn cắt Parabol (P) tại 2 điểm phân biệt A và B
b) Gọi Xa, Xb lần lượt là hoành độ giao điểm của đường thẳng (d) và parabol (P). Tìm giá trị của m để X^2aXb + x^2bXa-XaXb=3
chứng minh rằng với mọi giá trị của tham số m thì đường thẳng (d) : y = mx +1 luôn cắt Parabol (P) : y = x^2 tại hai điểm phân biệt. khi đó tìm m để y1 + y2 +y1*y2 = 7, với y1 , y2 là tung đọ của các giao điểm .
Cho Parabol(P) : y=x² và đường thăng (d) : y=(2m-1)x-m+2 ( m là tham số)
A) c)m rằng với mới m đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt
B)Tìm các giá trị m để đường thẳng (d) cắt Parabol (P) tại hai điểm phân biệt A(x1;y1);B(x2;y2) thoả mãn x1y1+x2y2=0
Trên mặt phẳng tọa độ Oxy cho parabol (P): y=x2 và đường thẳng (d): y=2mx+1 (m là tham số)
1) Chứng minh rằng với mọi m thì đường thẳng (d) và parabol (P) cắt nhau tại 2 điểm phân biệt.
2) Gọi giao điểm của đường thẳng (d) và parabol (P) là A và B. Chứng minh tam giác OAB vuông.
Cho Parabol (P) y=1/4 x^2 và đường thẳng (d) y=mx+1.
a, chứng minh với mọi giá trị của m đường thẳng (d) luôn cứt Parabol (P) tại hải điểm phân biệt.
b, Gọi A,B là giao điểm của (d) và (P). Tính diện tích OBA theo m (O là tung độ gốc)
Cho parabol ( P ) : y = x2 và đường thẳng ( d ) : y = ( 2 -m )x + m2 + 1 .
a/ Vẽ parabol ( P ) .
b/ Chứng minh rằng parabol ( P ) và đường thẳng ( d ) luôn cắt nhau tại hai điểm phân biệt A và B .
Cho parabol y=1/4x2 và đường thẳng y=mx +1 (d)
a) chứng minh với mọi giá trị của m đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt
b) gọi A và B là hai giao điểm (d) và (P) tính diện tích tam giác OAB theo m (O là gốc tọa độ)
Cho hàm số y= 2x^2 có đồ thị là parabol (P)
1. Tìm tọa độ giao điểm của parabol (P) với đường thẳng y= 3x-1
2. Đường thẳng y= 6x-4 cắt parabol (P) tại A và B. Tính SAOB
3. Trên parabol lấy 2 điểm A và B có hoành độ là -1 và 2. Viết PT đường thẳng AB
4. Tìm m để đường thẳng y= x+m tiếp xúc với parabol
5. Chứng minh đường thẳng y= mx-2m-5 cắt parabol tại 2 điểm phân biệt với mọi m
6. Tìm m để đường thẳng mx-2m+5 cắt parabol tại 2 điểm có hoành độ x1, x2 thỏa mãn x1^2 + x2^2 = 4