Question

Cho (O; R), đường kính AB. Kẻ OM vuông góc với AB (M thuộc (O)). Lấy I nằm giữa O và M; các tia AI, BI cắt đường tròn lần lượt tại K và N. a) Vẽ hình b) Chứng minh rằng tứ giác OINA nội tiếp c) Chứng minh rằng ^NOM = ^NBK

Answer 1

a:

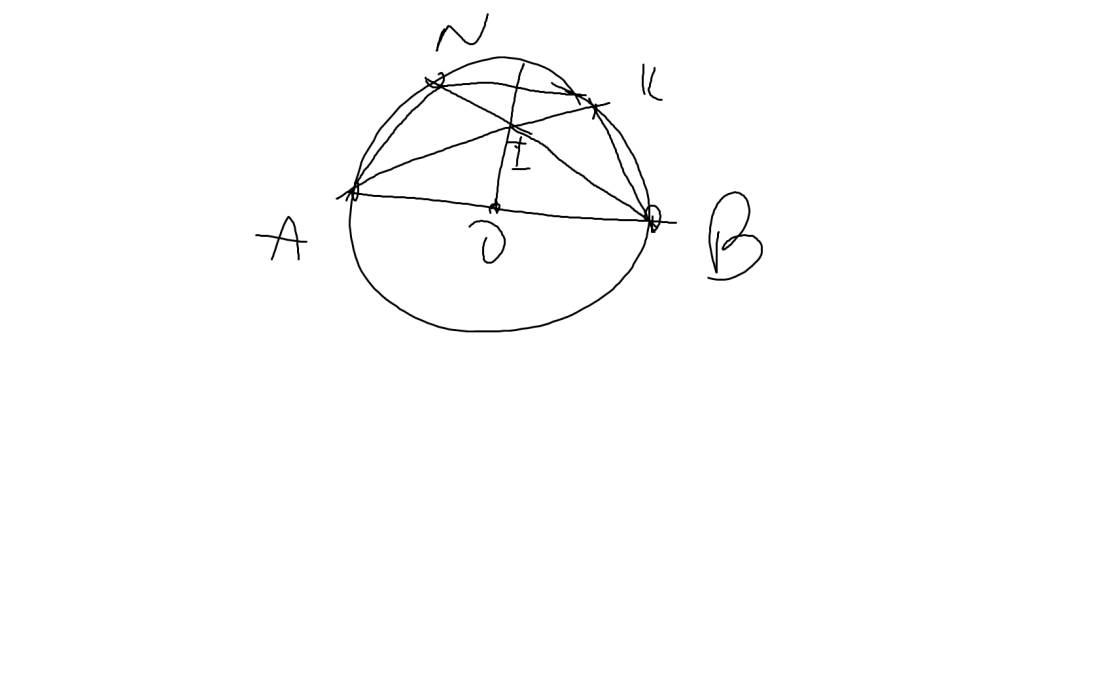
b: Xét (O) có

ΔANB nội tiếp

AB là đường kính

Do đó: ΔANB vuông tại N

Xét (O) có

ΔAKB nội tiếp

AB là đường kính

Do đó: ΔAKB vuông tại K

Xét tứ giác ANIO có \(\widehat{INA}+\widehat{IOA}=90^0+90^0=180^0\)

nên ANIO là tứ giác nội tiếp

b: Xét (O) có

\(\widehat{NAK}\) là góc nội tiếp chắn cung NK

\(\widehat{NBK}\) là góc nội tiếp chắn cung NK

Do đó: \(\widehat{NAK}=\widehat{NBK}\)

mà \(\widehat{NAK}=\widehat{NOM}\)(NAOI nội tiếp)

nên \(\widehat{NBK}=\widehat{NOM}\)