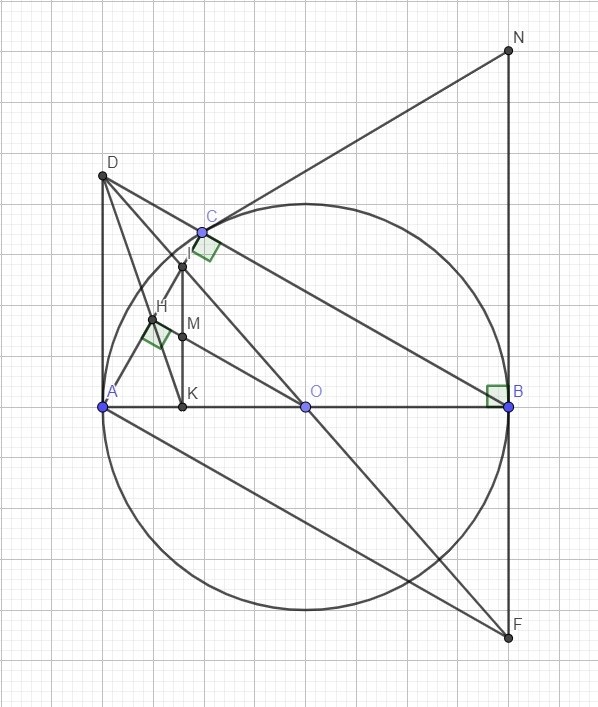
CHO (O) CÓ AB LÀ DG KÍNH . TRÊN (O) LẤY ĐIỂM C (AC <BC) . TIẾP TUYẾN TẠI A CỦA (O) CẮT TIA BC TẠI D . KẺ OH VUÔNG GÓC VỚI AC TẠI H
A) CM DA^2 =DB.DC
B) CM GÓC ODB =GÓC ADH
C) OD CẮT AC Ở M , TIA DH CẮT AB TẠI K .CM IK//AD
D) IK CẮT OH Ở M , CÁC TIẾP TUYẾN TẠI B,C CỦA (O) CẮT NHAU Ở N .CM 3 ĐIỂM A,M,N THẲNG HÀNG
Câu a em tự giải
Ta có 2 tam giác vuông ACD và BAD đồng dạng (chung góc D)
\(\Rightarrow\dfrac{AC}{AB}=\dfrac{AD}{BD}\Rightarrow\dfrac{2AH}{2OB}=\dfrac{AD}{BD}\Rightarrow\dfrac{AH}{OB}=\dfrac{AD}{BD}\) (1)
Lại có \(\widehat{DAH}=\widehat{OBD}\) (cùng phụ \(\widehat{ADB}\)) (2)
(1);(2) \(\Rightarrow\Delta ADH\sim\Delta BDO\left(c.g.c\right)\)
\(\Rightarrow\widehat{ODB}=\widehat{ADH}\)
c. Cũng từ trên ta suy ra \(\widehat{AHD}=\widehat{BOD}\)
Lại có \(\widehat{AHD}=\widehat{IHK}\) (đối đỉnh) \(\Rightarrow\widehat{BOD}=\widehat{IHK}\)
Mà \(\widehat{BOD}+\widehat{IOK}=180^0\Rightarrow\widehat{IHK}+\widehat{IOK}=180^0\)
\(\Rightarrow\) Tứ giác IHKO nội tiếp
\(\Rightarrow\widehat{IKO}=\widehat{IHO}=90^0\) hay \(IK\perp AB\)
\(\Rightarrow IK||AD\)
d.
Trong tam giác OIA có OH vuông góc AC và IK vuông góc AO
\(\Rightarrow\) M là trực tâm OIA
\(\Rightarrow AM\perp OI\) (3)
Qua A kẻ đường thẳng song song BC cắt tiếp tuyến tại B ở F
\(\Rightarrow ADBF\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow\) 2 đường chéo DF, AB cắt nhau tại trung điểm O của AB hay O, D, F thẳng hàng
Lại có ON là trung trực BC (\(NB=NC\) theo t/c 2 tiếp tuyến cắt nhau và \(OB=OC=R\))
\(\Rightarrow ON\perp BC\), mà \(BC||AF\Rightarrow ON\perp AF\)
\(\Rightarrow O\) là trực tâm tam giác ANF
\(\Rightarrow OF\perp AN\) (4)
(3);(4) \(\Rightarrow\) A;M;N thẳng hàng