Question

Cho O bất kì thuộc tam giác ABC. D,E,F là hình chiếu của O trên AB;BC;AC 

c/m AD²+ BE²+CF²=AF²+BD²+CE²

Answer 1

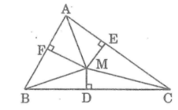
ΔADO vuông tại D

=>\(AD^2+DO^2=AO^2\)

=>\(AD^2=AO^2-OD^2\)

ΔAFO vuông tại F

=>\(AF^2+FO^2=AO^2\)

=>\(AF^2=AO^2-OF^2\)

ΔBDO vuông tại D

=>\(BD^2+DO^2=BO^2\)

=>\(BD^2=BO^2-OD^2\)

ΔBEO vuông tại E

=>\(EB^2+EO^2=BO^2\)

=>\(EB^2=BO^2-EO^2\)

ΔCEO vuông tại E

=>\(CE^2+EO^2=CO^2\)

=>\(CE^2=CO^2-OE^2\)

ΔCFO vuông tại F

=>\(CO^2=FO^2+FC^2\)

=>\(CF^2=CO^2-OF^2\)

\(AD^2+BE^2+CF^2\)

\(=OA^2-OD^2+OB^2-OE^2+OC^2-OF^2\)

\(=\left(OA^2-OF^2\right)+\left(OB^2-OD^2\right)+\left(OC^2-OE^2\right)\)

\(=AF^2+BD_{}^2+CE^2\)