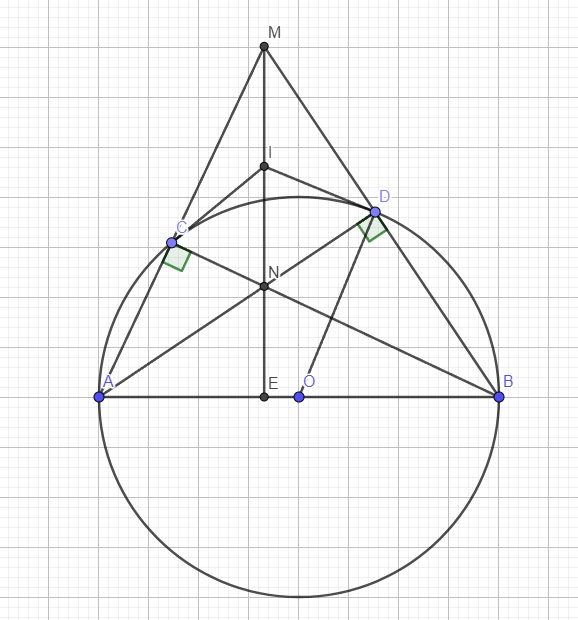
a.
Do AB là đường kính \(\Rightarrow\widehat{ACB}=\widehat{ADB}=90^0\)
\(\Rightarrow\widehat{MCN}=\widehat{MDN}=90^0\)
\(\Rightarrow C,D\) cùng nhìn MN dưới 1 góc vuông nên tứ giác MCND nội tiếp đường tròn đường kính MN
Mà I là trung điểm MN \(\Rightarrow I\) là tâm đường tròn ngoại tiếp MCND
\(\Rightarrow\widehat{CID}=2\widehat{CMD}\) (góc nt và góc ở tâm cùng chắn CD)
b.
Gọi E là giao điểm của MN và AB
Trong tam giác ABM, có \(\left\{{}\begin{matrix}AD\perp BM\\BC\perp AM\end{matrix}\right.\), mà AD và BC cắt nhau tại N
\(\Rightarrow N\) là trực tâm tam giác ABM
\(\Rightarrow ME\) là đường cao thứ 3 của tam giác ABM
\(\Rightarrow\widehat{MEB}=90^0\Rightarrow\widehat{EMB}+\widehat{EBM}=90^0\) (1)
\(OB=OD=R\Rightarrow\Delta OBD\) cân tại O \(\Rightarrow\widehat{EBM}=\widehat{ODB}\) (2)
I là tâm đường tròn ngoại tiếp MCND (cmt) \(\Rightarrow IM=ID\Rightarrow\Delta IDM\) cân tại I
\(\Rightarrow\widehat{EMB}=\widehat{IDM}\) (3)
(1);(2);(3) \(\Rightarrow\widehat{ODB}+\widehat{IDM}=90^0\)
\(\Rightarrow\widehat{IOD}=180^0-\left(\widehat{ODB}+\widehat{IDM}\right)=90^0\)
\(\Rightarrow ID\perp OD\)
\(\Rightarrow ID\) là tiếp tuyến của (O)