a) Nhận xét \(ACB=90^o\)( góc nội tiếp chắn nửa đường tròn ) nên \(AH\) vuông góc \(BC\)
\(\Rightarrow ACH=ABC\)
Mặt khác , ta lại có :
\(ACM=ABC\)
Từ đó \(ACH=ACM\) hay CA là tia phân giác của góc MCH

a) Nhận xét \(ACB=90^o\)( góc nội tiếp chắn nửa đường tròn ) nên \(AH\) vuông góc \(BC\)
\(\Rightarrow ACH=ABC\)
Mặt khác , ta lại có :
\(ACM=ABC\)
Từ đó \(ACH=ACM\) hay CA là tia phân giác của góc MCH
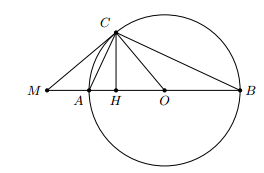
Cho nửa đường tròn tâm (o) đường kính AB.Trên tia đối của tia AB lấy một điểm M. Vẽ tiếp tuyến MC với nửa đường tròn. Gọi H là hình chiếu của C trên AB. a) Chứng minh rằng CA là tia phân giác của góc MCH. b,Chứng minh tam giác MAC và tam giác MCB đồng dạng .
Ai làm câu b giúp em với ạ
Cho nửa đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy một điểm M. Vẽ tiếp tuyến MC với nửa đường tròn. Gọi H là hình chiếu của C trên AB.
a) chứng minh rằng tia AC là tia phân giác của góc MCH
b) giả sử MA=a; MC=2a. Tính AB và CH theo a
Bài 1: TỪ một điểm M cố định bên ngoài dg tròn (O) ,kẻ một tiếp tuyến MT và một cát tuyến MAB của dg tròn đó
CM: MT^2= MA.MB
Bài 2: Cho nửa dg tròn (O) dg kính AB. Trên tia đối của tia AB lấy một điểm M vẽ tiếp tuyến MC với nửa dg tròn gọi là H là hình chiếu của C trên AB
a) CM: tam giác MAC đồng dạng tam giác MCB
b) CM :MA. MB=MO.MH
c) CM :CA là tia phân giác của góc MCH
Cho nửa đường tròn tâm O đường kính AB. Trên tia đối của tia AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn. Gọi H là hình chiếu của C trên AB.
a) CMR: tia CA là tia phân giác ∠MCH
b) giả sử MA=a, MC=2a. Tính AB và CH theo a
Cho nửa đường tròn (O) đường kính AB. Trên tia đối AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn . Gọi H là hình chiếu của C trên AB. CA là tia phân giác của góc nào dưới đây?
A. M C B ^
B. M C H ^
C. M C O ^
D. C M B ^
Cho nửa đường tròn (O) đường kính AB. Trên tia đối AB lấy điểm M. Vẽ tiếp tuyến MC với nửa đường tròn . Gọi H là hình chiếu của C trên AB. CA là tia phân giác của góc nào dưới đây?
A. M C B ^
B. M C H ^
C. M C O ^
D. C M B ^
Cho nửa đường tâm O , đường kính AB = 4 cm . Kẻ các tiếp tuyến Ax , By cùng phía với nửa đường tròn đối với AB . Gọi C là một điểm thuộc tia Ax . Kẻ tiếp tuyến CE với nửa đường tròn ( E là tiếp điểm ) , CE cắt By ở D .
a . Chứng minh rằng COOD = 90o ( Mình ko biết viết o ở trên không như trong sách ) .
b . Chứng minh rằng hình tam giác bằng chữ A ( ko biết viết hình ) AEB và hình tam giác bằng chữ A ( lại thế ) COD đồng dạng
c . Gọi I là trung điểm của CD . Vẽ đường tròn tâm I bán kính IC . Chứng minh rằng AB là tiếp tuyến của đường tròn ( i ) .
đ . Xác định vị trí của C trên tia Ax để có độ dài nhỏ nhất .
Bài 3. Cho tam giác ABC vuông ở A, với AC > AB. Trên AC lấy điểm M, vẽ đường tròn tâm O đường kính MC. Tia BM cắt đường tròn (O) tại D. Đường thẳng qua A và D cắt đường tròn (O) tại S. a) Chứng minh ABCD là tứ giác nội tiếp b) Chứng minh AC là tia phân giác của góc SCB c) Gọi E là giao điểm của BC với đường tròn (O). Chứng minh rằng các đường thẳng BA, EM, CD đồng quy. d) Chứng minh DM là tia phân giác của góc ADE e) Chứng minh M là tâm đường tròn nội tiếp tam giác ADE
Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiêp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP với đường tròn tâm O (tiếp điểm P khác điểm A) cắt By tại N
a, Chứng minh các tam giác MON và APB đồng dạng
b, Chứng minh AM.BN = R 2
c, Tính tỉ số S M O N S A P B khi AM = R 2
d, Tính thể tích của hình do nửa hình tròn đường kính AB quay một vòng quanh AB sinh ra