câu a tự làm ạ.
b. ΔCOD và ΔAMB đồng dạng => MC.MD = OM2
c, AC = R\(\sqrt{3}\)
BD.AC = MC.MD = OM2
=> BD = \(\dfrac{R\sqrt{3}}{3}\)
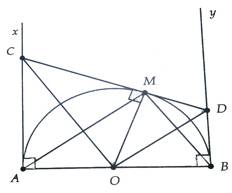
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên nửa đường tròn (M khác A, B) vẽ tiếp tuyên với nửa đường tròn, cắt Ax và By lần lượt tại C và D
a, Chứng minh ΔCOD và ΔAMB đồng dạng
b, Chứng minh MC.MD không đổi khi M di động trên nửa đường tròn
c, Cho biết OC = BA = 2R. Tính AC và BD theo R
Cho nửa đường tròn tâm O, đường kính AB. Kẽ các tiếp tuyến Ax, By cùng phía với nửa đường
tròn đối với AB. Từ điểm M trên nửa đường tròn kẽ tiếp tuyến thứ ba với đường tròn, nó cắt Ax và By lần
lượt tại C và D.
a/ Chứng minh: Tam giác COD là tam giác vuông.
b/ Chứng minh: MC.MD=\(OM^2\).
c/ Cho biết OC=BA=2R, tính AC và BD theo R.
Bài 2 Cho nửa đường tròn tâm O, đường kính AB. Kẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn đối với AB. Từ điểm M trên nửa đường tròn kẽ tiếp tuyến thứ ba với đường tròn , nó cắt Ax , By lần lượt tai C và D
a) chứng minh : Tam giác COD là tam giác vuông
b)Chứng minh : MC.MD=OM2
c) Cho biết OC=BA=2R, tính AC và BD theo R
Cho nửa đường tròn tâm O bán kính R, đường kính AB. Kẻ các tiếp tuyến Ax, By cùng phía với nửa đường tròn đối với AB. Từ điểm M trên nửa đường tròn kẻ tiếp tuyến thứ ba với đường tròn, tiếp tuyến này cắt Ax và By lần lượt tại C và D.
a) Chứng minh OC vuông góc AM và AM song song OD
b) chứng minh AC.BD = R^2
c) Chứng minh AB là tiếp tuyến đường tròn đường kính CD
d) Gọi K là giao điểm của AD và BC. Chứng minh MK vuông góc AB
Cho nửa hình tròn tâm O, đường kính AB. Kẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn đối với AB. Từ điểm M trên nửa đường tròn, nó cắt Ax và By lần lượt tại C và D.
a. CM: Tam giác COD là tam giác vuông.
b. CM: MC.MD = OM2
c. Cho biết OC=BA=2R, tính AC và BD theo R.
Bài 2: Cho nửa đường tròn tâm O, đường kính AB. Kẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn đối với AB. Từ điểm M trên nửa đường tròn kẽ tiếp tuyến thứ ba với đường tròn, nó cắt Ax và By lần lượt tại C và D.
a/ Chứng minh: Tam giác COD là tam giác vuông.
b/ Chứng minh: MC.MD=OM2.
c/ Cho biết OC=BA=2R, tính AC và BD theo R.
giup minh voi ah
Bài 1: Từ điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MA và MB (A,B là tiếp điểm ). Cho biết góc AMB bằng 400
a) Tính góc AOB
b) Từ O kẽ đường thẳng vuông góc OA cắt MB tại N. Chứng minh tam giác OMN là tam giác cân
Bài 2 Cho nửa đường tròn tâm O, đường kính AB. Kẽ các tiếp tuyến Ax, By cùng phía với nửa đường tròn đối với AB. Từ điểm M trên nửa đường tròn kẽ tiếp tuyến thứ ba với đường tròn , nó cắt Ax , By lần lượt tai C và D
a) chứng minh : Tam giác COD là tam giác vuông
b)Chứng minh : MC.MD=OM2
c) Cho biết OC=BA=2R, tính AC và BD theo R
Bài 3 : Cho hai đường tròn (O) và (O') tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O'). Đường tròn đường kính OC cắt (O) tại M và N
a)Đường thẳng CM cắt (O') tại P Chứng minh : OM////BP
b) Từ C kẽ đường thẳng vuông góc với CM cắt tia ON tại D . Chứng minh : Tam giác OCD là tam giác cân
Cho nửa đường tròn (O;R) đường kính AB. Trên cùng một nửa mặt phẳng bờ AB chứa nửa đường tròn vẽ các tia tiếp tuyến Ax, By. Lấy m thuộc nửa đường tròn ấy sao cho M# A và B. Tiếp tuyến với nửa đg tròn tại M cắt Ax và By lần lượt tại C và D.
a) Chứng minh rằng DC=AC+BD
b) chứng minh AB là tiếp tuyến của (I) đường kính CD
c) CMR tích AC.BD không đổi khi M di động trên nửa đg tròn
d) tìm vị trí của C trên Ax và D trên By để chu vi hình thang ABDC =14cm biết AB = 4cm
GIÚP MÌNH VỚI !!!
Cho nửa đường tròn (O; R) đường kính AB và một điểm E di động trên nửa đường tròn đó (E không trùng với A và B). Vẽ các tia tiếp tuyến Ax, By với nửa đường tròn. Tia AE cắt By tại C, tia BE cắt Ax tại D.a) Chứng minh rằng tích AD.BC không đổi. b) Tiếp tuyến tại E của nửa đường tròn cắt Ax, By theo thứ tự tại M và N. Chứng minh rằng ba đường thẳng MN, AB, CD đồng quy hoặc song song với nhau.c) Xác định vị trí của điểm E trên nửa đường tròn để diện tích tứ giác ABCD nhỏ nhất. Tính diện tích nhỏ nhất đó.
Cho nửa đường tròn tâm O , đường kính AB=2R , M là một điểm tùy ý nửa đường tròn ( M khác A;B ) . Kẻ hai tia tuyến Ax và By với đường tròn .Qua M kẻ tia tuyến thứ ba lần lượt cắt Ax và B tại C và D .
a, Chứng minh : CD =AC +BD và góc COD =90 độ.
b, Chứng minh : AC BD=R^2
C,OC cắt AM tại E ,OD cắt BM tại F . Chứng minh : EF=R
