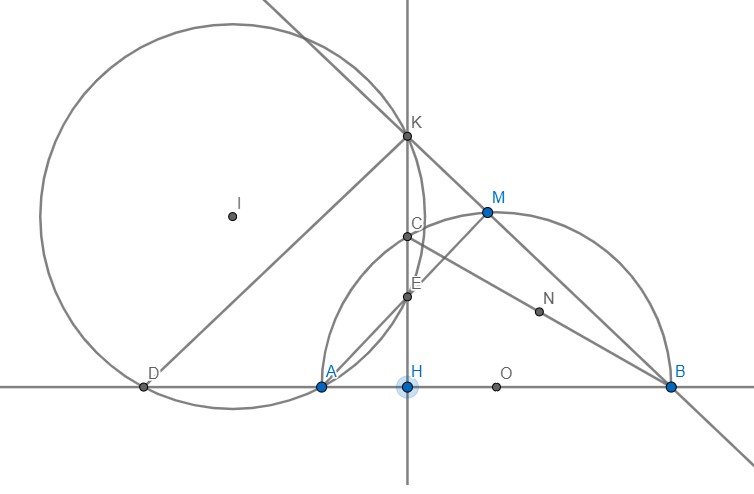
Cho nửa đường tròn tâm O đường kính AB. Lấy điểm H cố định trên đoạn OA, đường vuông góc với OA tại H cắt nửa đường tròn tại C. Gọi N là trung điểm của BC. M là điểm bất kì thuộc cung nhỏ BC (M ≠ B; M ≠ C). Tia BM cắt HC tại K; AM cắt HC tại E. Chứng minh rằng tâm I của đường tròn ngoại tiếp tam giác AEK di chuyển trên một đường thẳng cố định khi M di chuyển trên cung nhỏ BC.
AB cắt đường tròn ngoại tiếp tam giác AEK tại D
Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle EMB+\angle EHB=90+90=180\)
\(\Rightarrow EMBH\) nội tiếp \(\Rightarrow\angle KBD=\angle MBH=\angle AEH\)
Vì KEAD nội tiếp \(\Rightarrow\angle AEH=\angle KDB\Rightarrow\angle KBD=\angle KDB\)
\(\Rightarrow\Delta KDB\) cân tại K có KH là đường cao
\(\Rightarrow H\) là trung điểm BD mà B,H cố định \(\Rightarrow D\) cố định
Vì KEAD nội tiếp \(\Rightarrow I\in\) trung trực AD mà A,D cố định
\(\Rightarrow\) đpcm