Các câu hỏi tương tự
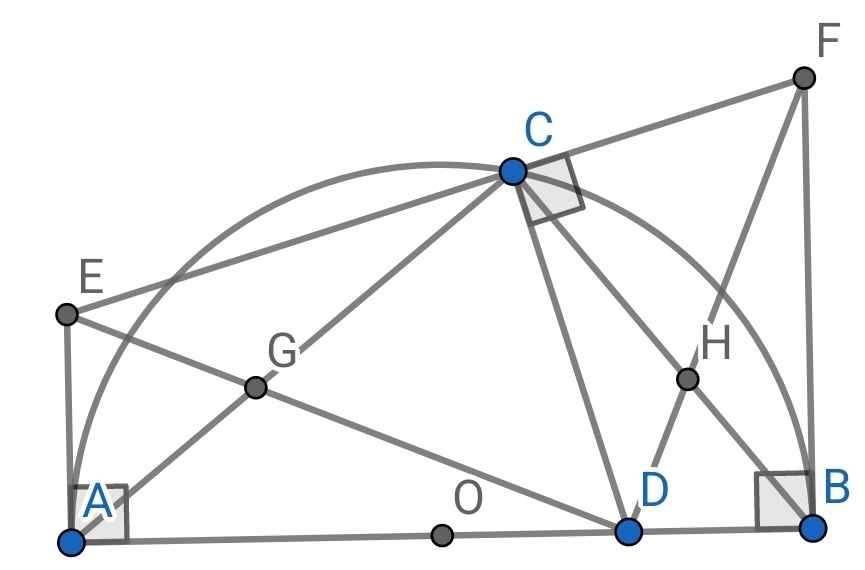
Bài 2. Cho nửa đường tròn (O; R), có BC là đường kính. Trên đoạn OC lấy điểm H (H khác C và O). Qua H kẻ đường thẳng vuông góc với BC cắt nửa đường tròn tại A. Gọi E và F là hình chiếu của H trên AB, AC. Gọi D là giao điểm của AH với EF.1) Chứng minh bốn điểm A, E, H, F cùng thuộc một đường tròn;2) Chứng minh OA vuông góc với EF;3) Qua B kẻ đường thẳng vuông góc với CB, cắt đường thẳng CD tại K. Chứng minh AK // EF.
Đọc tiếp
Bài 2. Cho nửa đường tròn (O; R), có BC là đường kính. Trên đoạn OC lấy điểm H (H khác C và O). Qua H kẻ đường thẳng vuông góc với BC cắt nửa đường tròn tại A. Gọi E và F là hình chiếu của H trên AB, AC. Gọi D là giao điểm của AH với EF.1) Chứng minh bốn điểm A, E, H, F cùng thuộc một đường tròn;2) Chứng minh OA vuông góc với EF;3) Qua B kẻ đường thẳng vuông góc với CB, cắt đường thẳng CD tại K. Chứng minh AK // EF.
Cho nửa đường tròn tâm O,đường kính AB. Lấy M nằm trên đường tròn (M khác A và B). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của đường tròn tâm O lần lược tại C và D. Gọi CD giao AB tại P. Gọi E là giao điểm của AM và BD. F là giao điểm của AC và BM. Chứng minh E,F,P thẳng hàng
Cho nửa đường tròn tâm O đường kính AB và tiếp tuyến Ax (A là tiếp điểm, Ax nằm ở nửa mặt phẳng chứa nửa đường tròn bò là AB). Trên đoạn AB lấy điểm M (M khác A, M khác B), đường thẳng vuông góc với AB tại M cắt nửa đường tròn tâm O tại C, tia BC cắt Ax tại D. Gọi N là trung điểm của AD. Gọi H là giao điểm của ON và AC. Kẻ HE vuông góc với AN (E thuộc AN). Đường tròn đường kính NC cắt EC tại F. Chứng minh NF luôn đi qua 1 điểm cố định khi M di chuyển trên AB.
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB và tiếp tuyến Ax (A là tiếp điểm, Ax nằm ở nửa mặt phẳng chứa nửa đường tròn bò là AB). Trên đoạn AB lấy điểm M (M khác A, M khác B), đường thẳng vuông góc với AB tại M cắt nửa đường tròn tâm O tại C, tia BC cắt Ax tại D. Gọi N là trung điểm của AD. Gọi H là giao điểm của ON và AC. Kẻ HE vuông góc với AN (E thuộc AN). Đường tròn đường kính NC cắt EC tại F. Chứng minh NF luôn đi qua 1 điểm cố định khi M di chuyển trên AB.
Cho nửa đường tròn tâm O đường kính AB, trên nửa đường tròn tâm O lấy điểm C, tên cung BC lấy điểm D, vẽ đường thẳng D vuông góc với AB tại B. Các đường thẳng AC và AD cắt D lần lượt tại E và F. CMR:
a) Tg CDFE nội tiếp.
b) Gọi I là trung điểm của BF. C/m: ID là tiếp tuyến của nửa đường tròn đã cho.
c) Đường thẳng CD cắt đường thẳng D tại K, tia phân giác goc CKE cắt AE và AF lần lượt tại M và N.C/m: Tam giác AMN cân.
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB, trên nửa đường tròn tâm O lấy điểm C, tên cung BC lấy điểm D, vẽ đường thẳng D vuông góc với AB tại B. Các đường thẳng AC và AD cắt D lần lượt tại E và F. CMR:
a) Tg CDFE nội tiếp.
b) Gọi I là trung điểm của BF. C/m: ID là tiếp tuyến của nửa đường tròn đã cho.
c) Đường thẳng CD cắt đường thẳng D tại K, tia phân giác goc CKE cắt AE và AF lần lượt tại M và N.C/m: Tam giác AMN cân.
Cho điểm A nằm ngoài đường tròn (O;R). Vẽ hai tiếp tuyến |AB,AC với đường tròn (O) (B,C là các tiếp điểm). Vẽ dường kính CD của đường tròn (O). AD cắt đường tròn (O) tại N (N khác D), gọi H là giao điểm của OA và BC. Gọi M là giao điểm của AD và BC, E là giao điểm của OA và CN. Đường thẳng vuông góc với ME cắt EN,BC,DC lần lượt tại F,P,Q.Cmr: PF=PQ
Cho đường tròn (O;R) đường kính AB. Trên tiếp tuyến tại A của (O;R) lấy điểm C sao cho AC 2R. Gọi D là giao điểm của BC và đường tròn (O)a) CM: AD là đường cao và cũng là đường trung tuyến của ΔABCb) Vẽ dây cung AE vuông góc với OC tại H. CM:CE là tiếp tuyến của đường tròn (O;R)c) Đường thẳng BE cắt đường thẳng OD tại F. Tính tanOBF và suy ra số độ của góc OFBd) Gọi K là hình chiếu của điểm E xuống AB, M là giao điểm của EK với BC. Tính độ dài các đoạn thẳng ME và MK theo R
Đọc tiếp
Cho đường tròn (O;R) đường kính AB. Trên tiếp tuyến tại A của (O;R) lấy điểm C sao cho AC = 2R. Gọi D là giao điểm của BC và đường tròn (O)
a) CM: AD là đường cao và cũng là đường trung tuyến của ΔABC
b) Vẽ dây cung AE vuông góc với OC tại H. CM:CE là tiếp tuyến của đường tròn (O;R)
c) Đường thẳng BE cắt đường thẳng OD tại F. Tính tanOBF và suy ra số độ của góc OFB
d) Gọi K là hình chiếu của điểm E xuống AB, M là giao điểm của EK với BC. Tính độ dài các đoạn thẳng ME và MK theo R
Cho nửa đường tròn (O), đường kính AB. M là một điểm bất kì trên cung AB. Tiếp tuyến tại M cắt tiếp tuyến tại A và B lần lượt tại C và D của đường tròn.a) CM: Tứ giác ACMO nội tiếpb) CM: góc CAM góc OPMc) Gọi P là giao điểm của CD và AB. CM: PA.POPC.PMd) Gọi E là giao điểm của AM và BD. F là giao điểm của AC và BM. CM: E, F, P thẳng hàng(Làm hộ t phần d nhá)
Đọc tiếp
Cho nửa đường tròn (O), đường kính AB. M là một điểm bất kì trên cung AB. Tiếp tuyến tại M cắt tiếp tuyến tại A và B lần lượt tại C và D của đường tròn.
a) CM: Tứ giác ACMO nội tiếp
b) CM: góc CAM = góc OPM
c) Gọi P là giao điểm của CD và AB. CM: PA.PO=PC.PM
d) Gọi E là giao điểm của AM và BD. F là giao điểm của AC và BM. CM: E, F, P thẳng hàng
(Làm hộ t phần d nhá)
Cho nửa đường tròn tâm O đường kính AB. Một điểm C di chuyển trên AO(khác A,O).Đường thẳng đi qua C vuông góc với AO cắt nửa đường tròn đã cho tại D.trên cung BD lấy điểm M(M Khác B và D).Tiếp tuyến của nửa đường tròn tại M cắt CD tại E. Gọi F là giao điểm của AM và CD.K là giao điểm của BM và CD.Gọi tâm Đường tròn ngoại tiếp tam giác AKF là I.Chứng minh rằng I luôn nằm trên một đường thẳng cố định khi C di chuyển trên AO.
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Một điểm C di chuyển trên AO(khác A,O).Đường thẳng đi qua C vuông góc với AO cắt nửa đường tròn đã cho tại D.trên cung BD lấy điểm M(M Khác B và D).Tiếp tuyến của nửa đường tròn tại M cắt CD tại E. Gọi F là giao điểm của AM và CD.K là giao điểm của BM và CD.Gọi tâm Đường tròn ngoại tiếp tam giác AKF là I.Chứng minh rằng I luôn nằm trên một đường thẳng cố định khi C di chuyển trên AO.
Cho nửa đường tròn tâm O đường kính AB = 2R . 1 điểm C cố định thuốc AO . Đường thẳng đi qua c vuông góc vs AO cắt nửa đường tròn tại D . Trên cung BD lấy điểm M . Tiếp tuyến của ( O ) tại M cắt CD tại E . Gọi f là giao điểm của AM và CD .
a , CMR tứ giác BCFM nội tiếp
b , CMR EM = EF
Cho nửa đường tròn (O),đường kính AB.Trên nửa đường tròn (O) lấy điểm G tùy ý (G khác A và B).Vẽ GH vuông góc với AB (H thuộc AB);trên đoạn thẳng HG lấy một điểm E (E khác H và G).Các tia AE và BE cắt nửa đường tròn (O) lần lượt tại C và D.Gọi F là giao điểm của hai tia BC và AD.Chứng minh rằng :a)Tứ giác ECFD nội tiếp được trong một đường trònb)Bốn điểm H,E,G,F thẳng hàngc)E là trung điểm của GH khi và chỉ khi G là trung điểm của FH
Đọc tiếp
Cho nửa đường tròn (O),đường kính AB.Trên nửa đường tròn (O) lấy điểm G tùy ý (G khác A và B).Vẽ GH vuông góc với AB (H thuộc AB);trên đoạn thẳng HG lấy một điểm E (E khác H và G).Các tia AE và BE cắt nửa đường tròn (O) lần lượt tại C và D.Gọi F là giao điểm của hai tia BC và AD.Chứng minh rằng :
a)Tứ giác ECFD nội tiếp được trong một đường tròn
b)Bốn điểm H,E,G,F thẳng hàng
c)E là trung điểm của GH khi và chỉ khi G là trung điểm của FH