a, HS tự chứng minh
b, Chứng minh được M N ⏜ = C A ⏜ = C B ⏜
=> ĐPCM

a, HS tự chứng minh
b, Chứng minh được M N ⏜ = C A ⏜ = C B ⏜
=> ĐPCM
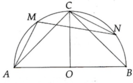
Cho nữa đường tròn (O), đường kính AB và C là điểm chính giữa của nửa đường tròn. Trên các cung CA và CB lần lượt lấy các điểm M và N sao cho cung CM = cung BN chứng minh"
a, AM = CN
b, MN = CA = CB
Cho nửa đường tròn (O) đường kính AB và điểm C nằm chính giữa của nửa đường tròn .Trên các cung CA và CB lần lượt lấy 2 điểm M,N sao cho cung Cm bằng cung BN>Cmr:
1, MN=CA=CB
Cho nửa đường tròn (O;R) đường kính AB và điểm C thuộc nửa đường tròn sao cho cung AC bằng hai lần cung CB. Gọi M và N là điểm chính giữa các cung AC và BC. Nối MN cắt AC tại I. Hạ ND vuông góc với AC, CB cắt NO tại E.
a, Tính góc MIC;
b) Chứng minh DN là tiếp tuyến của (O; R)
c) Cho R = 5cm. Tính độ dài cung CB và diện tích hình quạt OCB.
Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ đường tròn (7) tiếp xúc với (O) tại C và tiếp xúc với đường kính AB tại D
a, Nêu cách vẽ đường tròn (I) nói trên
b, Đường tròn (I) cắt cắt CA, CB lần lượt tại các điểm thứ hai là M, N. Chứng minh M, I, N thẳng hàng
c, Chứng minh đường thẳng CD đi qua điểm chính giữa nửa đường tròn (O) không chứa C
Cho nửa đường tròn O đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn . Gọi C là điểm trên nửa đường tròn sao cho cung CB = cung CA , D là 1 điểm tùy ý trên cung CB (D ≠ C, B) Các tia AC , AD cắt tia Bx theo thứ tự là E và F. Chứng minh tam giác ABC vuông cân. A
Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn .Vẽ một đường tròn (I) tiếp xúc với đường tròn (O) tại C và tiếp xúc với đường kính AB tại D, đường tròn này cắt CA và CB lần lượt tại các điểm thứ hai là M và N .Chứng minh rằng:
a, Ba điểm M,I,N thẳng hàng
b, ID vuông góc MN
Mình rất vội. Làm ơn giúp mình. Cảm ơn!
Cho nửa đường tròn (O) đường kính AB. Điểm C thuộc (O) sao cho CA < CB. Vói H là hình chiếu vuông góc của C trên AB, gọi D, M, N theo thứ tự là giao của đường tròn I đường kính CH với (O), AC và BC
a, Tứ giác CMHN là hình gì?
b, Chứng minh OC ⊥ MN
c, Với E = AB ∩ CD, chứng minh các điểm E, I, M và N thẳng hàng
d, Chứng minh ED.EC = EA.EB
Cho nửa đường tròn (O) đường kính AB kẻ tiếp tuyến Bx với nửa đường tròn, gọi C là điểm trên nửa đường tròn sao cho cung CB bằng cung CA. D là một điểm tùy ý trên cung CD (D khác C và B) Các tia AC, AD cắt tia Bx theo thứ tự E và F a, CM tam giác ABE vuông cân b, FB^2 = FD.FA c, CM AD.AF= AC.AE Giúp em với ạ. Cảm ơn ạ^^
Cho nửa đường tròn (O) đường kính AB=2R và điểm C nằm ngoài nửa đường tròn. CA cắt nửa đường tròn ở M, CB cắt nửa đường tròn ở N. Gọi H là giao điểm của AN và BM
a, chứng minh CH vuông góc AB
b, gọi I là trung điểm của CH. Chứng minh MI là tiếp tuyến của nửa đường tròn(O)
c, giả sử CH =2R. Tính số đo cung MN
( mọi người giúp mình với ạ )