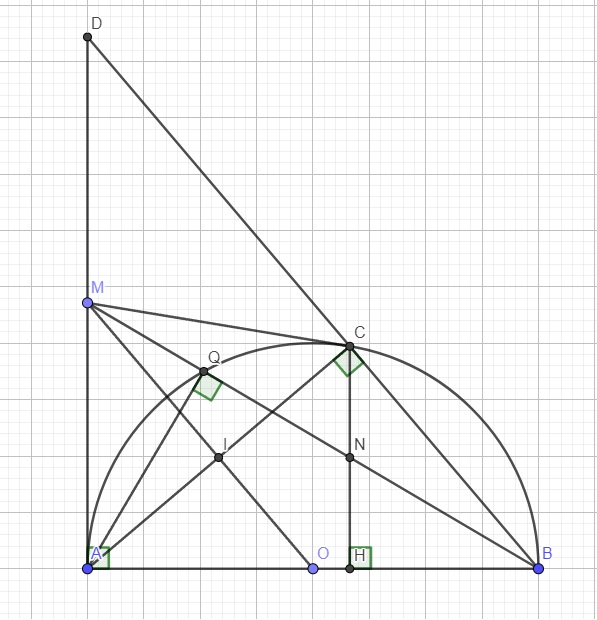
a.
Do MA là tiếp tuyến \(\Rightarrow\widehat{MAB}=90^0\)
Do AB là đường kính và Q thuộc đường tròn \(\Rightarrow\widehat{AQB}=90^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow\widehat{MQA}=90^0\)
Xét hai tam giác MQA và MAB có:
\(\left\{{}\begin{matrix}\widehat{AMQ}-chung\\\widehat{MQA}=\widehat{MAB}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta MQA\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{MQ}{MA}=\dfrac{MA}{MB}\Rightarrow MA^2=MQ.MB\)
b.
M là giao điểm 2 tiếp tuyến tại C và A \(\Rightarrow MA=MC\)
\(OA=OC=R\)
\(\Rightarrow OM\) là trung trực của AC
\(\Rightarrow OM\) vuông góc AC tại I hay \(\widehat{MIA}=90^0\)
\(\Rightarrow I\) và Q cùng nhìn AM dưới 1 góc vuông nên QIQM nội tiếp
c.
Kẻ BC kéo dài cắt Ax tại D
\(\widehat{ACB}=90^0\) (góc nt chắn nửa đường tròn) \(\Rightarrow AC\perp BD\)
\(\Rightarrow OM||BD\) (cùng vuông góc AC)
Mà O là trung điểm AB \(\Rightarrow OM\) là đường trung bình tam giác ABD
\(\Rightarrow\) M là trung điểm AD hay \(AM=MD\)
Do \(CH||AD\) (cùng vuông góc AB), áp dụng định lý Talet trong tam giác ABM:
\(\dfrac{BN}{BM}=\dfrac{NH}{AM}\)
Áp dụng định lý Talet trong tam giác DBM:
\(\dfrac{BN}{BM}=\dfrac{CN}{MD}\)
\(\Rightarrow\dfrac{NH}{AM}=\dfrac{CN}{MD}\Rightarrow NH=CN\) (do AM=MD theo cmt)