Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A
.
C
n
k
n
!
(
n
-
k
)
!
B
.
C
n
k
...
Đọc tiếp
Công thức tính số các chỉnh hợp chập k của một tập có n phần tử 1 ≤ k ≤ n là
A . C n k = n ! ( n - k ) !
B . C n k = n ! k ! ( n - k ) !
C . A n k = n ! ( n - k ) !
D . A n k = n ! k ! ( n - k ) !
Kí hiệu
A
n
k
là số các chỉnh hợp chập k của n phần tử
1
≤
k
≤
n
. Mệnh đề nào sau đây đúng? A.
A
n
k
n
!
(
n...
Đọc tiếp
Kí hiệu A n k là số các chỉnh hợp chập k của n phần tử 1 ≤ k ≤ n . Mệnh đề nào sau đây đúng?
A. A n k = n ! ( n + k ) !
B. A n k = n ! k ! ( n + k ) !
C. A n k = n ! k ! ( n - k ) !
D. A n k = n ! ( n - k ) !
Tìm số các chỉnh hợp chập k của một tập hợp gồm n phần tử
1
≤
k
≤
n
Đọc tiếp
Tìm số các chỉnh hợp chập k của một tập hợp gồm n phần tử 1 ≤ k ≤ n
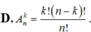
Với n là số nguyên dương thỏa mãn
A
n
k
+
2
A
n
2
100
(
A
n
k
là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa
x
5
trong khai triển của biểu thức...
Đọc tiếp
Với n là số nguyên dương thỏa mãn A n k + 2 A n 2 = 100 ( A n k là số các chỉnh hợp chập k của tập hợp có n phần tử). Số hạng chứa x 5 trong khai triển của biểu thức 1 + 3 x 2 n là:
A. 61236
B. 256 x 3
C. 252
D. 61236 x 3
biết n thuộc z , n lớn hơn 4 và chỉnh hợp chập hợp chập 0 của n trên 0 giai thừa, mỗi số gồm 5 chữ số khác nhau trong đó có đúng 2 chữ số lẻ và 2 chữ số lẻ đó đứng cạnh nhau.
A. 390
B. 630
C. 360
D. 436
Cho tập hợp X{0;1;2;3;4;5;6;7;8;9}, người ta lập 2 tập hợp con của X, tập hợp A{0;1;2;...;n} gồm n+1 số tự nhiên đầu tiên và B{n+1;n+2;...;2n}. Từ mỗi tập hợp A và B đó, người ta lập số tự nhiên có 5 chữ số đôi một khác nhau, trong số đó có hai chữ số hàng chục nghìn và hàng nghìn được viết bởi các chữ số lấy trong tập hợp A, 3 chữ số còn lại được lấy trong tập hợp B. Hỏi lập được bao nhiêu số tự nhiên như vậy và số lớn nhất là bao nhiêu?
Đọc tiếp
Cho tập hợp X={0;1;2;3;4;5;6;7;8;9}, người ta lập 2 tập hợp con của X, tập hợp A={0;1;2;...;n} gồm n+1 số tự nhiên đầu tiên và B={n+1;n+2;...;2n}. Từ mỗi tập hợp A và B đó, người ta lập số tự nhiên có 5 chữ số đôi một khác nhau, trong số đó có hai chữ số hàng chục nghìn và hàng nghìn được viết bởi các chữ số lấy trong tập hợp A, 3 chữ số còn lại được lấy trong tập hợp B. Hỏi lập được bao nhiêu số tự nhiên như vậy và số lớn nhất là bao nhiêu?
Viết công thức tính số chỉnh hợp chập k của n phần tử, công thức tính số tổ hợp chập k của n phần tử. Cho ví dụ.
Số các chỉnh hợp chập k của một tập hợp gồm n phần tử (với k,n
∈
ℕ
*
,
k
≤
n
).
A
.
k
!
(
k
-
n
)
!
B
.
C
n...
Đọc tiếp
Số các chỉnh hợp chập k của một tập hợp gồm n phần tử (với k,n ∈ ℕ * , k ≤ n ).
A . k ! ( k - n ) !
B . C n k . k ! .
C . C n k . ( n - k ) ! .
D . k ! ( n - k ) ! n !
Số các tổ hợp chập k của một tập hợp có n phần tử 1
≤
k
≤
n là :
A
.
C
n
k
n
!
(
n
-
k
)
!
B
.
C
n
k...
Đọc tiếp
Số các tổ hợp chập k của một tập hợp có n phần tử 1 ≤ k ≤ n là :
A . C n k = n ! ( n - k ) !
B . C n k = A n k k !
C . C n k = A n k ( n - k ) !
D . C n k = k ! ( n - k ) ! n !