Chọn C
Sử dụng công thức: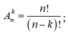 
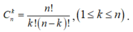
Ta có:
A
n
3
+
C
n
2
=
14
n
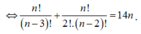
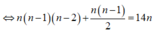
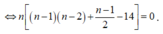
Tìm số hạng chứa x5 trong khai triển \(\left(x-\dfrac{2}{x}\right)^{n^{ }}\) , biết n là số tự nhiên thỏa mãn \(C^3_n=\dfrac{4}{3}n+2C^2_n\)
A.144 B.134 C.115 D.141
Cho hàm số f(n)= a n + 1 + b n + 2 + c n + 3 ( n ∈ N * ) với a, b, c là hằng số thỏa mãn a+b+c=0. Khẳng định nào sau đây đúng?
A. lim x → + ∞ f ( n ) = - 1
B. lim x → + ∞ f ( n ) = 1
C. lim x → + ∞ f ( n ) = 0
D. lim x → + ∞ f ( n ) = 2
Cho dãy số thỏa mãn u1 = 5; un+1 = 3un+ 4/3. Giá trị nhỏ nhất của n để u1 + u2 + … + un > 5100 - 2/3n là
A. 141
B. 142
C. 145
D. 146
Cho n ∈ N và n! = 1. Số giá trị của n thỏa mãn giả thiết đã cho là
A. 1.
B. 2.
C. 0.
D. Vô số.
Cho hàm số f(n)= 1+3+6+10+...+ n ( n + 1 ) 2 ( n ∈ N * ) .
Biết lim f ( n ) ( 3 n + 1 ) ( 5 n 2 + 2 ) = a b ( a , b ∈ Z ) phân số này tối giản. Giá trị b - 5a là
A.50
B.45
C.85
D.60
Cho khai triển nhị thức Niuton x 2 + 2 n x n với n n ∈ ℕ , x > 0. Biết rằng số
hạng thứ 2 của khai triển bằng 98 và n thỏa mãn A n 2 + 6 C n 3 = 36 n Trong các giá trị x sau, giá trị nào thỏa mãn?
A. 3
B. 4
C. 1
D. 2
Trong với n ∈ ℕ , n ≥ 2 và thỏa mãn 1 C 2 2 + 1 C 3 2 + 1 C 4 2 + . . . + 1 C n 2 = 9 5 . Tính giá trị của biểu thức P = C n 5 + C n + 2 3 ( n - 4 ) ! .
A. 61 90
B. 59 90
C. 29 45
D. 53 90
Cho hàm số f(n)= 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n . ( n + 1 ) . ( n + 2 ) = n ( n + 3 ) 4 ( n + 1 ) ( n + 2 ) , n ∈ N * . Kết quả giới hạn lim ( 2 n 2 + 1 - 1 ) f ( n ) 5 n + 1 = a b ( b ∈ Z ) . Giá trị của a 2 + b 2 là
A.101
B.443
C.363
D.402
tìm tất cả các bộ (n,k,p), với n,k là các số nguyên lớn hơn 1 và p là 1 số nguyên tố thỏa mãn \(n^5+n^4-2n^3-2n^2+1=p^k\)
