Các câu hỏi tương tự
Cho tứ diện ABCD có độ dài cạnh Ab thay đổi và AB x các cạnh còn lại bằng a không đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD là A.
3
a
3
4
B.
a
3
8
C.
3
a
3...
Đọc tiếp
Cho tứ diện ABCD có độ dài cạnh Ab thay đổi và AB = x các cạnh còn lại bằng a không đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD là
A. 3 a 3 4
B. a 3 8
C. 3 a 3 8
D. a 3 4
Cho tứ diện ABCD có AB x, tất cả các cạnh còn lại có độ dài bằng 2. Gọi S là diện tích tam giác ABC, h là khoảng cách từ D đến mp(ABC).Với giá trị nào của x thì biểu thức
V
1
3
S
.
h
đạt giá trị lớn nhất. A.
x
1
B.
x
6
C.
x
2
6
D....
Đọc tiếp
Cho tứ diện ABCD có AB = x, tất cả các cạnh còn lại có độ dài bằng 2. Gọi S là diện tích tam giác ABC, h là khoảng cách từ D đến mp(ABC).Với giá trị nào của x thì biểu thức V = 1 3 S . h đạt giá trị lớn nhất.
A. x = 1
B. x = 6
C. x = 2 6
D. x = 2
Cho khối tứ diện ABCD có
A
B
x
, tất cả các cạnh còn lại bằng 2. Thể tích khối tứ diện đã cho đạt giá trị lớn nhất bằng A.
1
2
B.
3
3
2
C.
2
2
3
D. 1
Đọc tiếp
Cho khối tứ diện ABCD có A B = x , tất cả các cạnh còn lại bằng 2. Thể tích khối tứ diện đã cho đạt giá trị lớn nhất bằng
A. 1 2
B. 3 3 2
C. 2 2 3
D. 1
Xét khối tứ diện ABCD có cạnh ADx và các cạnh còn lại đều bằng 2. Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất. A.
x
2
3
B.
x
6
C.
x
2
D.
x
3
Đọc tiếp
Xét khối tứ diện ABCD có cạnh AD=x và các cạnh còn lại đều bằng 2. Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất.
A. x = 2 3
B. x = 6
C. x = 2
D. x = 3
Xét tứ diện ABCD có các cạnh
A
B
B
C
C
D
D
A
1
và AC, BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng. A.
2
3
27
B.
4
3
27
C. ...
Đọc tiếp
Xét tứ diện ABCD có các cạnh A B = B C = C D = D A = 1 và AC, BD thay đổi. Giá trị lớn nhất của thể tích khối tứ diện ABCD bằng.
A. 2 3 27
B. 4 3 27
C. 2 3 9
D. 4 3 9
Xét khối tứ diện ABCD có cạnh ADx và các cạnh còn lại đều bằng
a
2
3
.
Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất A.
x
6
B.
x
14
C.
x
3
2
D.
x
2
3
Đọc tiếp
Xét khối tứ diện ABCD có cạnh AD=x và các cạnh còn lại đều bằng a = 2 3 . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất
A. x = 6
B. x = 14
C. x = 3 2
D. x = 2 3
Cho một khối tú diện có thể tích bằng V. Nấu tăng độ dài mỗi cạnh lên 2 lần thì thể tích khối tứ diện lúc đó bằng
A. 2V
B. V/2
C. 8V
D. V/8
Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhất. Gọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì
a
+
b
là: A.
5
+
5
3...
Đọc tiếp
Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhất.
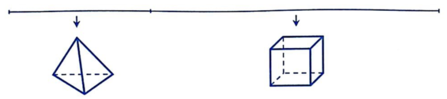
Gọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì a + b là:
A. 5 + 5 3 3
B. - 5 + 5 3 3
C. - 5 + 20 3 3
D. 5 + 20 3 3
Cho tứ diện ABCD có AB 1, còn tất cả các cạnh còn lại đều không lớn hơn 1. Thể tích của tứ diện ABCD đạt giá trị lớn nhất là A.
1
8
.
B.
1
4
.
C.
1
12
.
D.
1
3
.
Đọc tiếp
Cho tứ diện ABCD có AB > 1, còn tất cả các cạnh còn lại đều không lớn hơn 1. Thể tích của tứ diện ABCD đạt giá trị lớn nhất là
A. 1 8 .
B. 1 4 .
C. 1 12 .
D. 1 3 .