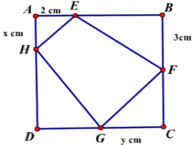
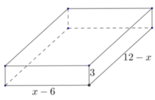
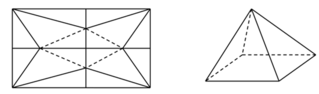
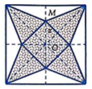
Ta có SEFGH nhỏ nhất ↔ S = S A E H + S C G F + S D G H lớn nhất
Tính được 2S= 2x+ 3y+ (6-x) (6-y) = xy-4x-3y+36 (1)
Mặt khác ∆ AEH đồng dạng ∆CGF nên A E C G = A H C F ⇒ x y = 6
Từ (1) và (2) suy ra 2S = 42 - ( 4 x - 18 x )
Ta có 2S nhỏ nhất khi và chỉ khi 4 x - 18 x nhỏ nhất.
Biểu thức nhỏ nhất 4 x - 18 x nhỏ nhất ↔ 4 x = 18 x ⇒ x = 3 2 2 ⇒ y = 2 2
Vậy x+y = 3 2 2 + 2 2
Chọn D.