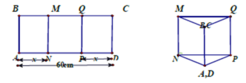
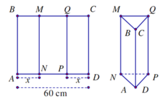
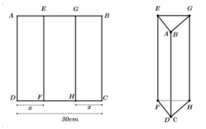
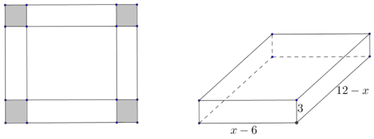
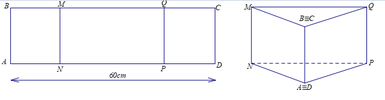
Cho một tấm nhôm hình chữ nhật ABCD có AD = 60 cm. Ta gập tấm nhôm theo hai cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau, với AN = PD (như hình vẽ dưới đây) để được một hình lăng trụ. Tìm độ dài đoạn AN để thể tích khối lăng trụ lớn nhất.
A. AN = 39 cm
B. AN = 20 cm
C. AN = 15 2 cm
D. AN = 15 cm
Đáp án B
Đặt AN = PD = x suy ra NP = AD-(AN + PD) = 60 - 2x
Gọi H là trung điểm của NP, tam giác ANP cân ⇒ A H ⊥ N P . Suy ra diện tích tam giác ANP là S ∆ A N P = 1 2 . A H . N P = 1 2 . A N 2 - N H 2 . N P = 1 2 A N 2 - N P 2 4 . N P = 1 2 . x 2 - 60 - 2 x 2 4 . 60 - 2 x = 1 2 . 60 x - 900 . 60 - 2 x . . Thể tích khối lăng trụ ANP.BMQ là V = A B . S ∆ A N P = A B . 15 x - 225 . 60 - 2 x . Xét hàm số f x = 30 - x x - 15 trên đoạn [15;30] suy ra m i n [ 15 ; 30 ] f x = 10 5 . Dấu bằng xảy ra khi và chỉ khi x = 20. Vậy độ dài AN = 20 cm.