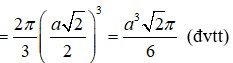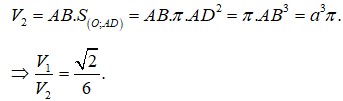Các câu hỏi tương tự
Trong không gian, cho hình chữ nhật ABCD có AB 2, AD 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d. A.
V
17
π
B.
V
5
π
C.
V
15
π
D.
V
30
π
Đọc tiếp
Trong không gian, cho hình chữ nhật ABCD có AB = 2, AD = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d.
A. V = 17 π
B. V = 5 π
C. V = 15 π
D. V = 30 π
Cho hình thang vuông ABCD có
A
⏞
D
⏞
90
∘
, ABAD2, CD2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB. A.
8
π
cm
3
B.
40
π
3
c
m
3
C. ...
Đọc tiếp
Cho hình thang vuông ABCD có A ⏞ = D ⏞ = 90 ∘ , AB=AD=2, CD=2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.
A. 8 π cm 3
B. 40 π 3 c m 3
C. 8 π 3 c m 3
D. 16 π 3 c m 3
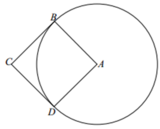
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC. A.
1000
π
+
375
π
2
6
B.
1000
π
+...
Đọc tiếp
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC.
A. 1000 π + 375 π 2 6
B. 1000 π + 375 π 2 6
C. 500 π + 125 π 2 6
D. 500 π + 375 π 2 6
Cho hình thang cân ABCD có các cạnh AB2a, CD4a và cạnh bên ADBC3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD xung quanh trục đối xứng của nó. A.
V
4
3
π
a
3
B.
V
4
+
10
2
3...
Đọc tiếp
Cho hình thang cân ABCD có các cạnh AB=2a, CD=4a và cạnh bên AD=BC=3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD xung quanh trục đối xứng của nó.
A. V = 4 3 π a 3
B. V = 4 + 10 2 3 π a 3
C. V = 10 2 3 π a 3
D. V = 14 2 3 π a 3
Cho hình thang cân ABCD có các cạnh đáy AB 2a, CD 4a và cạnh bên AD BC 3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó. A.
V
4
3
πa
3
B.
V
4
+
10
2
3
πa
3
C....
Đọc tiếp
Cho hình thang cân ABCD có các cạnh đáy AB = 2a, CD = 4a và cạnh bên AD = BC = 3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
A. V = 4 3 πa 3
B. V = 4 + 10 2 3 πa 3
C. V = 10 2 3 πa 3
D. V = 14 2 3 πa 3
Trong không gian cho ABCD là hình chữ nhật, AB2, AD1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết
d
(
A
B
,
d
)
d
(
C
D
,
d
)
. Tính a biết rằng thể t...
Đọc tiếp
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Cho hình thang cân
A
B
C
D
;
A
B
/
/
C
D
;
A
B
2
;
C
D
4.
Khi quay hình thang quanh trục CD thu được một khối tròn xoay có thể tích bằng
6
π
.
Diện tích hình thang ABCD bằng: A.
9
2
B....
Đọc tiếp
Cho hình thang cân A B C D ; A B / / C D ; A B = 2 ; C D = 4. Khi quay hình thang quanh trục CD thu được một khối tròn xoay có thể tích bằng 6 π . Diện tích hình thang ABCD bằng:
A. 9 2
B. 9 4
C. 6
D. 3
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y sinx.cosx, trục tung, trục hoành và đường thẳng x π/2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox. A. V π/16. B.
V
π
2
16
C.
V
π
2
+
π...
Đọc tiếp
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y =sinx.cosx, trục tung, trục hoành và đường thẳng x =π/2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V =π/16.
B. V = π 2 16
C. V = π 2 + π 16
D. V = π 2 4
Cho hình thang vuông ABCD như hình vẽ. Biết
A
B
2
a
,
A
C
a
13
,
B
D
a
10
. Lần lượt quay tam giác ABC; BCD quay trục BC ta được các khối tròn xoay
T
1
v
à
T
2
. Tính phần thể tích V chung của k...
Đọc tiếp
Cho hình thang vuông ABCD như hình vẽ. Biết A B = 2 a , A C = a 13 , B D = a 10 . Lần lượt quay tam giác ABC; BCD quay trục BC ta được các khối tròn xoay T 1 v à T 2 . Tính phần thể tích V chung của khối T 1 v à T 2 .
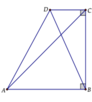
A. V = π a 3 .
B. V = 3 π a 3 .
C. V = 4 9 π a 3 .
D. V = 2 3 π a 3 .