\(\dfrac{d_1}{d_2}=\left|\dfrac{\overrightarrow{IM}}{\overrightarrow{IN}}\right|=\dfrac{4}{3}\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Đường thẳng d:yx-3 cắt đồ thị (C) của hàm số
y
x
+
1
x
-
2
tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng
△
:
x
-
y
0
Tính dd1+d A. B. C. d 6 D.
Đọc tiếp
Đường thẳng d:y=x-3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d1, d2 lần lượt là khoảng cách từ A và B đến đường thẳng △ : x - y = 0 Tính d=d1+d
A.![]()
B. ![]()
C. d = 6
D. ![]()
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
2
+
t
y
1
−
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x = 2 + t y = 1 − t z = 2 t và d 2 : x = 2 − 2 t y = 3 z = t . Khoảng cách từ điểm M − 2 ; 4 ; − 1 đến mặt phẳng cách đều hai đường thẳng d 1 và d 2 là:
A. 15 15
B. 2 15 15
C. 30 15
D. 2 30 15
Trong không gian Oxyz, cho hai đường thẳng
d
1
:
x
-
1
1
y
+
2
1
z
-
1
2
và
d...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 2 1 = z - 1 2
và d 2 : x - 1 2 = y - 1 1 = z + 2 1 . Mặt phẳng (P) : x + ay + bz + c = 0 song song
với d 1 , d 2 và khoảng cách từ d 1 đến (P) bằng 2 lần khoảng cách từ d 2 đến (P).
Giá trị của a + b + c bằng
A. 6
B. 14
C. -4
D. -6
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng
d
1
:
x
-
1
1
y
+
1
1
z
-
3
-
1
;
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng d 1 : x - 1 1 = y + 1 1 = z - 3 - 1 ; d 2 : x - 1 1 = y + 2 1 = z - 2 1 . Viết phương trình đường thẳng d song song với mặt phẳng (P):2x+3y+4z-6=0, cắt đường thẳng d1, d2 lần lượt tại M và N sao cho A M ⇀ . A N ⇀ = 5 và điểm N có hoành độ nguyên.
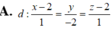
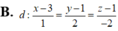
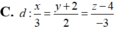
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
1
3
y
+
2
-
1
z
+
1
2
;
d
2
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d 1 : x - 1 3 = y + 2 - 1 = z + 1 2 ; d 2 : x = 3 t y = 4 - t z = 2 + 2 t
và mặt phẳng Oxz cắt d 1 , d 2 lần lượt tại các điểm A, B.
Diện tích S của tam giác OAB bằng
A. S = 5
B. S = 3
C. S = 6
D. S = 10
Trong không gian với hệ trục tọa độ Oxyz, cho ba đường thẳng
d
1
:
x
1
y
-
1
z
t
1...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho ba đường thẳng d 1 : x = 1 y = - 1 z = t 1 , d 2 : x = t 2 y = - 1 z = 0 , d 3 : x = 1 y = t 3 z = 0 Viết phương trình mặt phẳng đi qua M(1;2;3) và cắt ba đường thẳng d1, d2, d3 lần lượt tại A, B, C sao cho M là trực tâm tam giác ABC
![]()
![]()
![]()
D. đáp án khác
Trong không gian tọa độ Oxyz cho đường thẳng
d
1
và
d
2
lần lượt có phương trình
x
9
+
2
t
y
-
1
-...
Đọc tiếp
Trong không gian tọa độ Oxyz cho đường thẳng d 1 và d 2 lần lượt có phương trình x = 9 + 2 t y = - 1 - t z = 3 - t và x = 1 - 2 t ' y = 4 + t ' z = 2 + t ' Viết phương trình mặt phẳng chứa cả hai đường thẳng d 1 và d 2
![]()
![]()
![]()
![]()
Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng
d
1
,
d
2
lần lượt có phương trình
d
1
:
x
-
2
2
y
-
2
1
z
-
3
3
,
d...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng d 1 , d 2 lần lượt có phương trình d 1 : x - 2 2 = y - 2 1 = z - 3 3 , d 2 : x - 1 2 = y - 2 - 1 = z - 1 4 . Phương trình mặt phẳng (P) cách đều hai đường thẳng d1;d2 là:
A. 7x – 2y - 4z = 0.
B. 7x – 2y - 4z + 3 = 0.
C. 2x+ y + 3z + 3 = 0
D. 14x – 4y – 8z + 3 = 0
Cho hàm số yf(x) có đạo hàm tại x1. Gọi d1,d2 lần lượt là tiếp tuyến của đồ thị hàm số yf(x) và yg(x)x . f(2x-1) tại điểm có hoành độ x1 Biết rằng hai đường thẳng d1,d2 vuông góc với nhau. Khẳng định nào dưới đây đúng. A.
f
(
1
)
2
B.
2...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm tại x=1. Gọi d1,d2 lần lượt là tiếp tuyến của đồ thị hàm số y=f(x) và y=g(x)=x . f(2x-1) tại điểm có hoành độ x=1 Biết rằng hai đường thẳng d1,d2 vuông góc với nhau. Khẳng định nào dưới đây đúng.
A. f ( 1 ) < 2
B. 2 ≤ f ( 1 ) ≤ 2 2
C. 2 ≤ f ( 1 ) ≤ 2
D. f ( 1 ) ≥ 2 2
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;3;-2) và hai đường thẳng
d
1
:
x
-
1
2
y
-
2
3
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;3;-2) và hai đường thẳng d 1 : x - 1 2 = y - 2 3 = z 1 , d 2 : x + 1 - 1 = y - 1 2 = z - 2 4 . Đường thẳng d qua M cắt d 1 , d 2 lần lượt tại A và B. Độ dài đoạn thẳng AB bằng
A. 3
B. 2
C. 6
D. 5




