Chọn đáp án A

Xét thiết diện qua trục của hình nón N là ∆ A B C cân tại A.
Theo định lí hàm số sin ta có
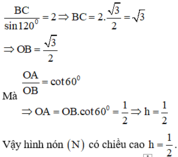
Chọn đáp án A

Xét thiết diện qua trục của hình nón N là ∆ A B C cân tại A.
Theo định lí hàm số sin ta có
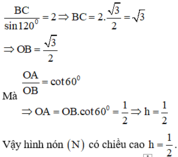

Cho hình nón xoay có đường cao h = 4, bán kính đáy r = 3. Mặt phẳng (P) đi qua đỉnh của hình nón nhưng không qua trục của hình nón và cắt hình nón theo giao tuyến là một tam giác cân có độ dài cạnh đáy bằng 2. Tính diện tích S của thiết diện được tạo ra.
A. S = 91
B. S = 2 3
C. S = 19
D. S = 2 6
Cho hình nón tròn xoay có đường cao h = 5 , bán kính đáy r = 3. Mặt phẳng (P) qua đỉnh của hình nón nhưng không qua trục của hình nón và cắt hình nón theo giao tuyến là một tam giác cân có độ dài cạnh đáy bằng 4. Gọi O là tâm của hình tròn đáy. Tính khoảng cách d từ điểm O đến mặt phẳng (P).
A. d = 5 2
B. d = 10
C. d = 5
D. d = 10 2
Cho hình nón có bán kính đường tròn đáy bằng a. Thiết diện qua trục hình nón là một tam giác cân có góc ở đáy bằng 45 ° Tính thể tích khối cầu ngoại tiếp hình nón
A. 1 3 π a 3
B. 8 3 π a 3
C. 4 3 π a 3
D. 4 π a 3
Cho hình nón tròn xoay có chiều cao bằng 4 và bán kính đáy bằng 3. Mặt phẳng (P) đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là một tam giác cân có độ dài cạnh đáy bằng 2. Diện tích của thiết diện bằng
A. 6
B. 19
C. 2 6
D. 2 3
Cho một hình nón có góc ở đỉnh bằng 90 ° và bán kính đáy bằng 4. Khối trụ (H) có một đáy thuộc đáy của hình nón và đường tròn đáy của mặt đáy còn lại thuộc mặt xung quanh của hình chóp. Biết chiều cao của (H) bằng 1. Tính thể tích của (H)
A. V H = 9 π
B. V H = 6 π
C. V H = 18 π
D. V H = 3 π
Cho hình nón (N) có đường sinh tạo với đáy một góc 60 ∘ . Mặt phẳng qua trục của (N) cắt (N) được thiết diện là một tam giác có bán kính đường tròn ngoại tiếp bằng 2. Thế tích V của khối nón (N).
A . V = 9 3 π
B . V = 3 π
C . V = 9 π
D . V = 3 3 π
Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM = x (0 < x < h). (C) là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Giá trị x theo h để thể tích khối nón đỉnh O đáy là (C) lớn nhất là:
A. x = h 2
B. x = h 2 2
C. x = h 3 2
D. x = h 3
Cho hình nón (N) có đường cao SO=h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt O M = x , 0 < x < h . C là thiết diện của mặt phẳng (P) vuông góc với trục SO tại M, với hình nón (N). Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất.
A. h/2
B. h 2 2
C. h 3 2
D. h/3
Cho hình nón có đỉnh S, chiều cao h và bán kính đáy bằng R. Mặt phẳng α qua S cắt hình nón tạo ra một thiết diện tam giác. Diện tích lớn nhất của thiết diện bằng
A. h 2 + R 2 2
B. h 2 + R 2 4
C. h 2 + R 2 3
D. h 2 + R 2 2