\(V=\dfrac{4}{3}\pi R^3=288\pi\Rightarrow R=6\)
\(\Rightarrow S_{max}=\pi R^2=36\pi\)
cho mặt cầu (s) tâm o và có thể tích là 288π. mặt phẳng (P) cắt (S) tại (C) và khoảng cách từ tâm (S) đến (P) là 2 căn 5 thì bán kính của đường tròn (C) là
cho mặt cầu (s) tâm o và có thể tích là 288π. đường thẳng denta cắt (s)=ab và ab=. khoảng cách từ tâm (s) đến đường thẳng denta là
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó. Xác định h để thể tích của hình nón là lớn nhất.
Cho khối cầu (S) có tâm I và bán kính R= 2 3 , gọi (P) là mặt phẳng cắt khối cầu (S) theo thiết diện là hình tròn (C) . Tính khoảng cách d từ I đến (P) sao cho khối nón có đỉnh I và đáy là hình tròn (C) có thể tích lớn nhất.
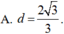
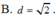
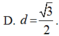
cho mặt cầu (S) có tâm O và bán kính R. biết diện tích của (S) là 36π. thể tích của (S) là
Cho mặt cầu (S) tâm O, bán kính R = 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).
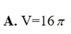
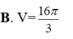
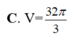
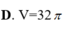
Cho mặt cầu (S) tâm O, bán kính bằng 2. (P) là mặt phẳng cách O một khoảng bằng 1 và cắt (S) theo một đường tròn (C). Hình nón (N) có đáy là (C), đỉnh thuộc (S), đỉnh cách (P) một khoảng lớn hơn 2. Kí hiệu V 1 , V 2 lần lượt là thể tích của khối cầu (S) và khối nón (N). Tỉ số V 1 V 2 là
Trong không gian Oxyz, cho mặt cầu (S): ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 3 ) 2 = 48 Gọi ( α ) là mặt phẳng đi qua hai điểm A(0;0-4), B(2;0;0) và cắt (S) theo giao tuyến là đường tròn (C). Khối nón (N) có đỉnh là tâm của (S), đường tròn đáy là (C) cỏ thể tích lớn nhất bằng
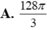
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của khối nón đỉnh S đáy là hình tròn tâm O' bằng bao nhiêu, biết rằng thể tích của nó bằng 1 8 thể tích khối nón đỉnh S, đáy là hình tròn tâm O.
