Đáp án A
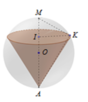
Theo bài ra, ta có khối nón (N) nội tiếp khối cầu (S).
Giả sử khối nón (N) có đỉnh A, tâm đáy I như hình vẽ bên với h = I A là chiều cao và bán kính đáy r = I K
Tam giác AMK vuông tại K, có I K 2 = I A . I M ⇔ r 2 = h 2 R − h
Suy ra V N = 1 3 π r 2 h = π 3 h 2 2 R − h = π 3 . 2 R h 2 − h 3
Xét hàm số f h = 2 R h 2 − h 3 trên khoảng 0 ; 2 R → max f h = 32 R 3 27
Vậy thể tích cần tính là V = π 3 . 32 R 3 27 = 32 π R 3 81



