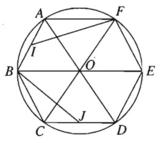
a) Phép quay tâm O góc 120 ο biến F, A, B lần lượt thành B, C, D; biến trung điểm I của AB thành trung điểm J của CD. Nên nó biến tam giác AIF thành tam giác CJB.
b) Phép quay tâm E góc 60 ο biến A, O, F lần lượt thành C, D, O.

a) Phép quay tâm O góc 120 ο biến F, A, B lần lượt thành B, C, D; biến trung điểm I của AB thành trung điểm J của CD. Nên nó biến tam giác AIF thành tam giác CJB.
b) Phép quay tâm E góc 60 ο biến A, O, F lần lượt thành C, D, O.
Cho lục giác đều ABCDEF tâm O. Tìm ảnh của tam giác AOF.
a. Qua phép tịnh tiến theo vectơ AB
b. Qua phép đối xứng qua đường thẳng BE.
c. Qua phép quay tâm O góc quay 120 o .
Trong mặt phẳng Oxy cho các điểm A(-3;2), B(-4;5) và C(-1;3).
a. Chứng minh rằng các điểm A’(2;3), B’(5;4) và C’(3;1) theo thứ tự là ảnh của A, B và C qua phép quay tâm O góc – 90 o .
b. Gọi tam giác A 1 B 1 C 1 là ảnh của tam giác ABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc – 90 o và phép đối xứng qua trục Ox. Tìm tọa độ các đỉnh của tam giác A 1 B 1 C 1 .
Trong mặt phẳng tọa độ Oxy, cho các điểm A (1;1), B(0;3), C(2;4) .Xác định ảnh của tam giác ABC qua các phép biến hình sau.
(a)Phép tịnh tiến theo vector v = (2;1).
(b)Phép đối xứng qua trục Ox
(c)Phép đối xứng qua tâm I(2;1).
(d)Phép quay tâm O góc 90 o .
(e)Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trụ Oy và phép vị tự tâm O tỉ số k = -2
Cho hình chữ nhật ABCD. Gọi O là tâm đối xứng của nó. Gọi I, F, J, E lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tìm ảnh của tam giác AEO qua phép đồng dạng có được từ việc thực hiện liên tiếp phép đối xứng qua đường thẳng IJ và phép vị tự tâm B, tỉ số 2.
Cho tam giác ABC và điểm O. Xác định ảnh của tam giác đó qua phép quay tâm O góc 60o.
Cho lục giác ABCDEF đều tâm O(O là tâm đường tròn ngoại tiếp). Ta thực hiện phép quay tâm O, góc quay φ biến lục giác ABCDEF thành chính nó. Một số đo của góc φ là
A. 45 0
B. 30 0
C. 90 0
D. 120 0
Cho hình vuông ABCD tâm O.
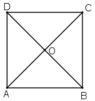
a. Tìm ảnh của điểm C qua phép quay tâm A góc 90 o .
b. Tìm ảnh của đường thẳng BC qua phép quay tâm O góc 90 o
1. Cho hình bình hành ABCD có tâm O, Gọi M, N lần lượt là trung điểm của AB, AO.
a) XĐ ảnh của tam giác AND qua phép tịnh tiến \(\overrightarrow{OC}\)
b)XĐ ảnh của tam giác AMN qua phép vị tự tâm O, tỉ số -2
2. trong mặt phẳng Oxy cho điểm M(1;-5),\(\overrightarrow{v}=\left(-2,1\right)\)đường thẳng d: x-4y+3=0,
đường tròn \(\left(C\right):\left(x+2\right)^2+\left(y-1\right)^2=5\)
a) tìm tọa độ M' là ảnh của M qua phép tịnh tiến vecto \(\overrightarrow{v}\)
b)Viết phương trình d' là ảnh của d qua phép quay tâm O, góc quay \(^{-90^o}\)
c) tìm phương trình (C') là ảnh của (C) qua phép vị tự tâm O, tỉ số 2.
3.
Cho đường thẳng (d): x-5y-4=0. Viết phương trình đường thẳng (d') ảnh của (d) qua phép vị tự tâm O , góc 90o và phép vị tự tâm I(-2,3) tỉ số -3
Cho hình vuông ABCD tâm O. Xác định ảnh của tam giác OBC qua phép quay tâm O góc quay 90°. a. Tam giácOCB b.tam giácOCD c.tam giácOAD d.tam giácOAB