Các câu hỏi tương tự
Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay
α
.
Tìm
α
.
A.
α
60
°
B.
α
−
60
°
C.
α
120
°
D.
α
−
120
°
Đọc tiếp
Cho lục giác đều ABCDEF tâm O như hình bên.
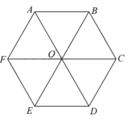
Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay α . Tìm α .
A. α = 60 °
B. α = − 60 °
C. α = 120 °
D. α = − 120 °
Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay α . Tìm α.
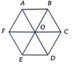
A. 30°
B. 60°
C. 90°
D. 120°
Cho hình chóp S.ABC có
S
A
⊥
A
B
C
và
Δ
A
B
C
vuông tại C. Gọi O là tâm đường tròn ngoại tiếp tam giác
S
B
C
.
H
là hình chiếu vuông góc của O lên (ABC). Khẳng định nào sau đây đúng? A. H là tâm đường tròn nội tiếp tam giác
Δ
A
B
C...
Đọc tiếp
Cho hình chóp S.ABC có S A ⊥ A B C và Δ A B C vuông tại C. Gọi O là tâm đường tròn ngoại tiếp tam giác S B C . H là hình chiếu vuông góc của O lên (ABC). Khẳng định nào sau đây đúng?
A. H là tâm đường tròn nội tiếp tam giác Δ A B C
B. H là trọng tâm tam giác Δ A B C
C. H là trung điểm cạnh AB
D. H là trung điểm cạnh AC
Trong mặt phẳng với hệ tọa độ
Ox
y
cho đường thẳng
Δ
:
x
+
2
y
−
6
0.
Viết phương trình đường thẳng
Δ
là ảnh của đường thẳng
Δ
qua phép quay tâm O góc
90
∘
A.
2
x
−
y
+
6
0
B.
2...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Ox y cho đường thẳng Δ : x + 2 y − 6 = 0. Viết phương trình đường thẳng Δ ' là ảnh của đường thẳng Δ qua phép quay tâm O góc 90 ∘
A. 2 x − y + 6 = 0
B. 2 x − y − 6 = 0
C. 2 x + y + 6 = 0
D. 2 x + y − 6 = 0
Cho hàm số
y
2
x
−
1
x
−
2
có đồ thị (C) Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến
Δ
của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến của
Δ
của (C)tạo với hai trục tọa độ một tam giác có di...
Đọc tiếp
Cho hàm số y = 2 x − 1 x − 2 có đồ thị (C) Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến Δ của (C) tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến của Δ của (C)tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào
A. (27;28)
B. (28;29)
C. (26;27)
D. (29;30)
Cho tứ diện ABCD có đáy BCD là tam giác đều, trọng tâm G.
Δ
là đường thẳng qua G và vuông góc với (BCD). A chạy trên
Δ
sao cho mặt câu ngoại tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích khối ABCD là: A.
a
3
12
B.
a
3
2
12
C....
Đọc tiếp
Cho tứ diện ABCD có đáy BCD là tam giác đều, trọng tâm G. Δ là đường thẳng qua G và vuông góc với (BCD). A chạy trên Δ sao cho mặt câu ngoại tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích khối ABCD là:
A. a 3 12
B. a 3 2 12
C. a 3 3 12
D. a 3 3 6
Cho hàm số
y
x
3
+
3
x
2
−
1
có đồ thị (C). Gọi Δ là tiếp tuyến của (C) tại điểm có hoành độ
x
0
0
, B là giao điểm thứ hai của Δ với (C). Tính diện tích tam giác OAB. A.
1
4
. B.
3
2
. C....
Đọc tiếp
Cho hàm số y = x 3 + 3 x 2 − 1 có đồ thị (C). Gọi Δ là tiếp tuyến của (C) tại điểm có hoành độ x 0 = 0 , B là giao điểm thứ hai của Δ với (C). Tính diện tích tam giác OAB.
A. 1 4 .
B. 3 2 .
C. 1 2 .
D. 2.
Cho (O ; R), đường kính AB. Trên đường tròn lấy điểm C sao cho BC bằng R. Từ B vẽ tiếp tuyến với đường tròn, tiếp tuyến này cắt đường thẳng AC tại Da, Cm tam giác ACB vuông tại C?b, Tính AC , BD theo R.c, Vẽ đường tròn ngoại tiếp tam giác CBD, gọi O là tâm đường tròn này. Cm OC là tiếp tuyến của (O) và AB là tiếp tuyến của (O).d, Gọi I là tâm đường tròn nội tiếp tam giác ABD. Tính OI theo R.
Đọc tiếp
Cho (O ; R), đường kính AB. Trên đường tròn lấy điểm C sao cho BC bằng R. Từ B vẽ tiếp tuyến với đường tròn, tiếp tuyến này cắt đường thẳng AC tại D
a, Cm tam giác ACB vuông tại C?
b, Tính AC , BD theo R.
c, Vẽ đường tròn ngoại tiếp tam giác CBD, gọi O' là tâm đường tròn này. Cm O'C là tiếp tuyến của (O) và AB là tiếp tuyến của (O').
d, Gọi I là tâm đường tròn nội tiếp tam giác ABD. Tính OI theo R.
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;2;-1),B(2;0;1),C(-2;2;3). Đường thẳng
Δ
nằm trong mặt phẳng (ABC) qua trực tâm H của tam giác ABC và cùng tạo với các đường thẳng AB, AC một góc
α
45
°
có một véctơ chỉ phương là
u
→
(a;b;c) với c là một số nguyên tố. Giá trị của biểu thức ab+bc+ca bằng A. -67. B. 23. B. -33. B. -37.
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;2;-1),B(2;0;1),C(-2;2;3). Đường thẳng Δ nằm trong mặt phẳng (ABC) qua trực tâm H của tam giác ABC và cùng tạo với các đường thẳng AB, AC một góc α < 45 ° có một véctơ chỉ phương là u → (a;b;c) với c là một số nguyên tố. Giá trị của biểu thức ab+bc+ca bằng
A. -67.
B. 23.
B. -33.
B. -37.