Phương pháp
Tính chiều cao lăng trụ dựa vào định lý Pytago
Tính thẻ tích lăng trụ V = S.h với S là diện tích đáy và h là chiều cao lăng trụ
Cách giải:
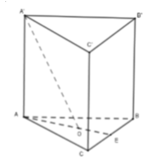
Gọi E là trung điểm của BC.

Chọn A
Phương pháp
Tính chiều cao lăng trụ dựa vào định lý Pytago
Tính thẻ tích lăng trụ V = S.h với S là diện tích đáy và h là chiều cao lăng trụ
Cách giải:

Gọi E là trung điểm của BC.

Chọn A
Cho lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của điểm A′ lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC, biết O A ' = a . Tính theo a thể tích V của khối lăng trụ đã cho.
A. 3 a 3 4 .
B. 3 a 3 3 .
C. 3 a 3
D. 3 a 3 12
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có góc giữa hai mặt phẳng (A′BC) và (ABC) bằng 60 0 , cạnh AB = 2. Thể tích V của khối lăng trụ ABC.A′B′C′ là
A. 3 3 4
B. 3
C. 3
D. 3 3
Cho hình lăng trụ tam giác đều ABCA’B’C’ có cạnh đáy bằng a, khoảng cách từ tâm O của tam giác đều ABC đến mặt phẳng (A'BC) bằng a/6. Tính thể tích V của khối lăng trụ ABCA’B’C’
A. V = a 3 3 3 16
B. V = a 3 2 6
C. V = a 3 3 2 16
D. V = a 3 3 6
Cho hình lăng trụ đứng ABC.A' B' C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a và A' B = 3a. Tính thể tích của khối lăng trụ ABC.A' B' C'.
A. 2 2 a 3
B. 5 a 3 3
C. 2 2 a 3 3
D. 5 a 3
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, hình chiếu của A’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° Tính thể tích khối lăng trụ ABC.A’B’C’
A. a 3 3 4
B. 4 a 3 3
C. 2 a 3 3
D. a 3 3 2
Cho hình lăng trụ đứng ABC.A’B’C’ biết đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A’BC) bằng a/6. Tính thể tích khối lăng trụ ABC.A’B’C’.
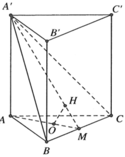
A. 3 a 3 2 16
B. 3 a 3 2 4
C. 3 a 3 2 28
D. 3 a 3 2 8
Cho khối lăng trụ ABC.A′B′C′ có đáy là tam giác vuông cân tại A, BC = 2a và hình chiếu vuông góc của A′ lên mặt phẳng (ABC) trùng với trung điểm cạnh BC, góc giữa AA′ và mặt đáy bằng 60 ° . Thể tích khối lăng trụ đã cho bằng
A. 3 a 3 3
B. a 3 2
C. 3 a 3 2
D. 3 a 3
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh AB=a,AA'=2a . Hình chiếu của 'A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là:
A. a 3 11 4
B. a 3 11 12
C. a 3 47 8
D. a 3 4
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A′ xuống mặt phẳng ABC trùng với trung điểm của cạnh AB. Mặt bên (ACC′A′) tạo với đáy một góc 60 0 . Tính thể tích khối lăng trụ ABC.A′B′C′.
A. 3 a 3 2
B. 3 a 3 3 2
C. a 3 3 2
D. a 3 3 3
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, độ dài cạnh bên bằng 2 a 3 , hình chiếu của đỉnh A’ trên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ bằng
A. a 3 3 36 .
B. a 3 3 6 .
C. a 3 3 12 .
D. a 3 3 24 .