Đáp án B
Ta có V I . A B C V A B C . A ' B ' C ' = 1 3 d ( I , A B C ) ) . S A B C A ' A . S A B C
Mà A ' I I C = A ' M A C = 1 2 ⇒ I C A ' C = 2 3
⇒ d ( I , ( A B C ) ) A ' A = 2 3
⇒ V I . A B C V A B C . A ' B ' C ' = 2 9
Đáp án B
Ta có V I . A B C V A B C . A ' B ' C ' = 1 3 d ( I , A B C ) ) . S A B C A ' A . S A B C
Mà A ' I I C = A ' M A C = 1 2 ⇒ I C A ' C = 2 3
⇒ d ( I , ( A B C ) ) A ' A = 2 3
⇒ V I . A B C V A B C . A ' B ' C ' = 2 9
Cho hình lăng trụ đứng ABC.A’B’C’. Gọi M là trung điểm A’C’, I là giao điểm của AM và A'C. Khi đó tỉ số thể tích của khối tứ diện IABC với khối lăng trụ đã cho bằng:
A. 2 3
B. 2 9
C. 4 9
D. 1 2
Cho lăng trụ tam giác đều ABC.A’B’C’. Trên A’B, kéo dài lấy điểm M sao cho B'M= 1 2 A'B'. Gọi N, P lần lượt là trung điểm của A’C’ và B’B. Mặt phẳng (MNP) chia khối lăng trụ ABC.A’B’C’ thành hai khối đa diện trong đó khối đa diện chứa đỉnh A’ có thể tích V 1 và khối đa diện chứa đỉnh C’ có thể tích V 2 . Tính V 1 V 2 .
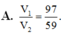
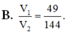
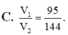
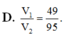
Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A’C’, BB’. Thể tích của khối tứ diện CMNP bằng:
A. 5 24 V
B. 1 4 V
C. 7 24 V
D. 1 3 V
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A’ lên (ABC) là trung điểm cạnh AB, góc giữa đường thẳng A’C và mặt đáy bằng 60 0 . Tính thể tích khối lăng trụ đã cho.
A. 3 a 3 3 8 .
B. a 3 3 8 .
C. 3 a 3 3 16 .
D. 3 a 3 8 .
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Mặt bên ABB’A’ có diện tích bằng a 2 3 . Gọi M; N lần lượt là trung điểm của A’B; A’C . Tính tỉ số thể tích của hai khối chóp A’. AMN và A’.ABC.
A. 1 2
B. 1 3
C. 1 4
D. 1 5
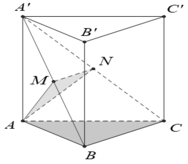
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại B, A B = a , A C = a 3 , đường thẳng A’C tạo với đáy một góc 450. Tính thể tích V của khối lăng trụ ABC.A’B’C’
![]()
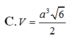
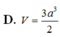
Cho lăng trụ ABC.A'B'C'; M, N lần lượt là trung điểm A'B' và A’C’. Gọi V1, V2 là thể tích của hai phần lăng trụ bị chia ra bởi mặt phẳng (BCNM). Tính tỉ số V 1 V 2
A. V 1 V 2 = 5 7
B. V 1 V 2 = 3 4
C. V 1 V 2 = 1
D. V 1 V 2 = 1 2
Cho hình lăng trụ đứng ABC.A’B’C’ có A B = 1 , A C = 2 , B A C ^ = 120 0 . Giả sử D là trung điểm của cạnh CC’ và B D A ' ^ = 90 0 . Tính thể tích V của khối lăng trụ ABC.A’B’C’
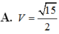
![]()
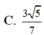
![]()
Cho hình lăng trụ ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của BB’ và CC’. Mặt phẳng (AEF) chia khối lăng trụ thành 2 phần có thể tích V1 và V2 như hình vẽ. Khi đó tỉ số V 1 V 2 có giá trị là
A. 1 4
B. 1 2
C. 1 3
D. 3 4