Các câu hỏi tương tự
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a. Mặt phẳng (ABC) tạo với mặt đáy góc
60
0
. Tính theo a thể tích lăng trụ ABC.A’B’C’
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc 60 0 . Tính theo a thể tích lăng trụ ABC.A’B’C’
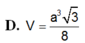
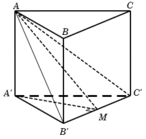
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cạnh a, A’B tạo với mặt phẳng đáy góc 600. Thể tích khối lăng trụ ABC.A’B’C’ bằng
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác cạnh a, A’B tạo với mặt phẳng đáy góc 600. Thể tích khối lăng trụ ABC.A’B’C’ bằng
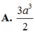
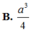
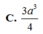
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông tại A; AB3, AC3. Mặt phẳng (ABC) hợp với (ABC) góc
60
0
. Thể tích lăng trụ đã cho bằng bao nhiêu?
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông tại A; AB=3, AC=3. Mặt phẳng (A'BC) hợp với (A'B'C') góc 60 0 . Thể tích lăng trụ đã cho bằng bao nhiêu?
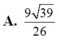
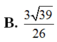
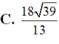
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC a,
ACB
^
60°. Đường chéo B’C tạo với mặt phẳng (AA’C’C) một góc 30°. Tính thể tích của khối lăng trụ theo a. A.
a
3
15
3
B.
a
3
6
C. ...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC = a, ACB ^ = 60°. Đường chéo B’C tạo với mặt phẳng (AA’C’C) một góc 30°. Tính thể tích của khối lăng trụ theo a.
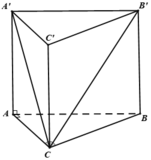
A. a 3 15 3
B. a 3 6
C. a 3 15 12
D. a 3 15 24
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1,
A
A
3
. Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC)
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1, A A ' = 3 . Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC)
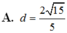
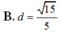
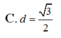
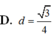
Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC a
3
; BC 3a,
A
C
B
^
30°. Cạnh bên hợp với mặt phẳng đáy góc 60° và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Thể tích khối lăng trụ ABC.A’B’C’ bằng: A.
4
a...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC = a 3 ; BC = 3a, A C B ^ = 30°. Cạnh bên hợp với mặt phẳng đáy góc 60° và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Thể tích khối lăng trụ ABC.A’B’C’ bằng:
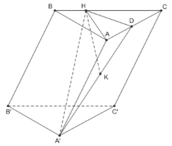
A. 4 a 3 9
B. 19 a 3 4
C. 9 a 3 4
D. 4 a 3 19
Cho lăng trụ tam giác ABC.A’B’C’ đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc H của A’ trên mặt phẳng (ABC) trùng với trực tâm của tam giác ABC. Tất cả các cạnh bên đều tạo với mặt phẳng đáy góc 60°. Thể tích của khối lăng trụ ABC.A’B’C’là: A.
a
3
3
4
B.
a
3...
Đọc tiếp
Cho lăng trụ tam giác ABC.A’B’C’ đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc H của A’ trên mặt phẳng (ABC) trùng với trực tâm của tam giác ABC. Tất cả các cạnh bên đều tạo với mặt phẳng đáy góc 60°. Thể tích của khối lăng trụ ABC.A’B’C’là:
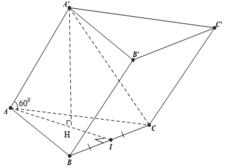
A. a 3 3 4
B. a 3 3 6
C. a 3 3 2
D. a 3 2 2
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với ABACa,
∠
B
A
C
120
°
, mặt phẳng (A’BC’) tạo với đáy một góc
60
°
. Tính thể tích của khối lăng trụ đã cho bằng: A.
3
3...
Đọc tiếp
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với AB=AC=a, ∠ B A C = 120 ° , mặt phẳng (A’BC’) tạo với đáy một góc 60 ° . Tính thể tích của khối lăng trụ đã cho bằng:
A. 3 3 a 3 8
B. 9 a 3 8
C. a 3 3 8
D. 3 a 3 8