Các câu hỏi tương tự
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1,
A
A
3
. Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC) A.
d
2
15
5
B.
d
15
5
C.
d
3
2
D. ...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1, A A ' = 3 . Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC)
A. d = 2 15 5
B. d = 15 5
C. d = 3 2
D. d = 3 4
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A’BC) bằng A.
a
2
2
B.
a
6
4
C.
a
21
2...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A’BC) bằng
A. a 2 2
B. a 6 4
C. a 21 2
D. a 3 4
Cho lăng trụ tam giác
A
B
C
.
A
B
C
có khoảng cách từ A đến mặt phẳng
A
B
C
bằng 6a Khoảng cách từ trung điểm M của cạnh
B
C
đến mặt phẳng
A
B
C
bằng A. 6a B. 2a C. 4a D. 3a
Đọc tiếp
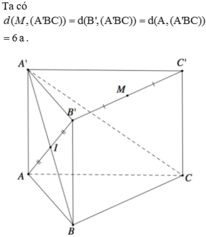
Cho lăng trụ tam giác A B C . A ' B ' C ' có khoảng cách từ A đến mặt phẳng A ' B C bằng 6a Khoảng cách từ trung điểm M của cạnh B ' C ' đến mặt phẳng A ' B C bằng
A. 6a
B. 2a
C. 4a
D. 3a
Cho hình lăng trụ đứng ABC.A’B’C’ biết đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A’BC) bằng a/6. Tính thể tích khối lăng trụ ABC.A’B’C’. A.
3
a
3
2
16
B.
3
a
3
2...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ biết đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A’BC) bằng a/6. Tính thể tích khối lăng trụ ABC.A’B’C’.
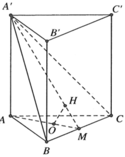
A. 3 a 3 2 16
B. 3 a 3 2 4
C. 3 a 3 2 28
D. 3 a 3 2 8
Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đấy bằng a, khoảng cách từ A đến mặt phẳng (A’BC) bằng
a
3
Tính thể tích lăng trụ. A.
3
3
a
3
B.
3
a
3
4
C.
2
a
3...
Đọc tiếp
Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đấy bằng a, khoảng cách từ A đến mặt phẳng (A’BC) bằng a 3 Tính thể tích lăng trụ.
A. 3 3 a 3
B. 3 a 3 4
C. 2 a 3 4
D. 3 a 3 2
Cho lăng trụ đứng tam giác đều ABC.A’B’C’ có cạnh đáy bằng a. Gọi I là trung điểm của B’C’. Tính khoảng cách từ điểm B tới mặt phẳng (AA’I)
A. a/3
B. a
C. a/2
D. a/4
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 300. Hình chiếu H của A trên mặt phẳng (A’B’C’) là trung điểm của B’C’. Tính theo a khoảng cách giữa hai mặt phẳng đáy của lăng trụ ABC.A’B’C’. A.
a
2
B.
a
3
C.
a
3...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 300. Hình chiếu H của A trên mặt phẳng (A’B’C’) là trung điểm của B’C’. Tính theo a khoảng cách giữa hai mặt phẳng đáy của lăng trụ ABC.A’B’C’.
A. a 2
B. a 3
C. a 3 2
D. a 2 2
Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a; chiều cao bằng 2a . Mặt phẳng (P) qua B’ và vuông góc A’C chia lăng trụ thành hai khối. Tính khoảng cách từ điểm A đến (P). A.
9
a
5
10
B.
7
a
5
5
C.
7
a
5...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a; chiều cao bằng 2a . Mặt phẳng (P) qua B’ và vuông góc A’C chia lăng trụ thành hai khối. Tính khoảng cách từ điểm A đến (P).
A. 9 a 5 10
B. 7 a 5 5
C. 7 a 5 10
D. 3 a 5 10
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng a3 .Gọi M là trung điểm của CC’. Tính khoảng cách từ điểm A’ đến mặt phẳng (ABM) biết rằng ABM là tam giác đều cạnh a A. 4a/3 B.
4
a
3
3
C. 2a/3 D.
4
3
a...
Đọc tiếp
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng a3 .Gọi M là trung điểm của CC’. Tính khoảng cách từ điểm A’ đến mặt phẳng (ABM) biết rằng ABM là tam giác đều cạnh a
A. 4a/3
B. 4 a 3 3
C. 2a/3
D. 4 3 a 3