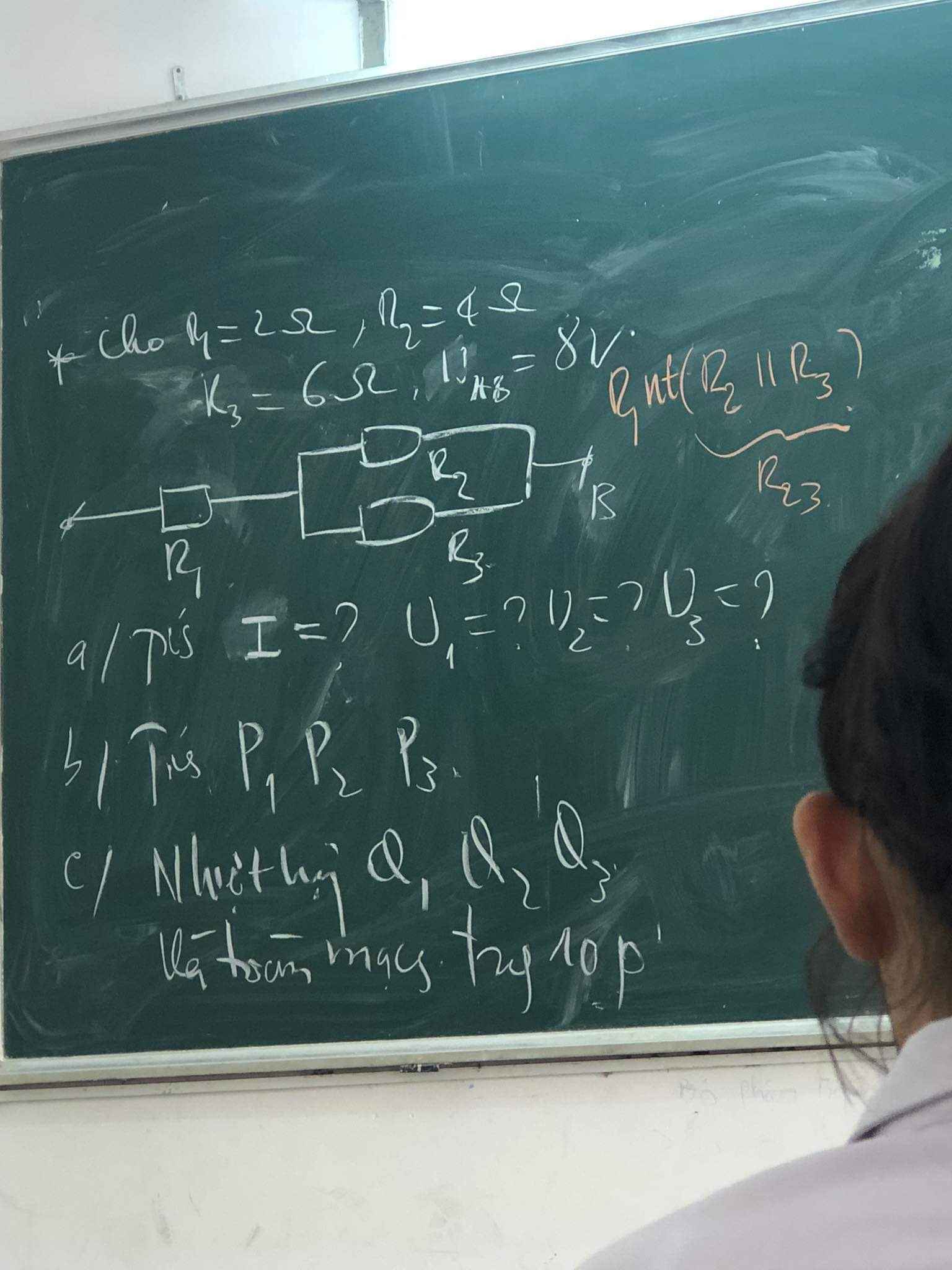\(MCD:R_1nt\left(R_2//R_3\right)\)
\(\Rightarrow R=R_1=\dfrac{R_2R_3}{R_2+R_3}=2+\dfrac{4\cdot6}{4+6}=4,4\Omega\)
\(\Rightarrow I=\dfrac{U}{R}=\dfrac{8}{4,4}=\dfrac{20}{11}A\)
\(\Rightarrow\left\{{}\begin{matrix}U_1=I_1R_1=\dfrac{20}{11}\cdot2=\dfrac{40}{11}V\\U_{23}=U_2=U_3=U-U_1=8-\dfrac{40}{11}=\dfrac{48}{11}V\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}P_1=U_1I_1=\dfrac{40}{11}\cdot\dfrac{20}{11}=\dfrac{800}{121}\\P_2=\dfrac{U_2^2}{R_2}=\dfrac{\left(\dfrac{48}{11}\right)^2}{4}=\dfrac{576}{121}\\P_3=\dfrac{U_3^2}{R_3}=\dfrac{\left(\dfrac{48}{11}\right)^2}{6}=\dfrac{384}{121}\end{matrix}\right.\)(W)
\(\Rightarrow\left\{{}\begin{matrix}Q_1=P_1t=\dfrac{800}{121}\cdot10\cdot60=3966,9\left(J\right)\\Q_2=P_2t=\dfrac{576}{121}\cdot10\cdot60=2856,2\left(J\right)\\Q_3=P_3t=\dfrac{384}{121}\cdot10\cdot60=1904,13\left(J\right)\\Q=UIt=8\cdot\dfrac{20}{11}\cdot10\cdot60=8727,27\left(J\right)\end{matrix}\right.\)