Các câu hỏi tương tự
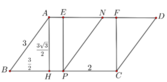
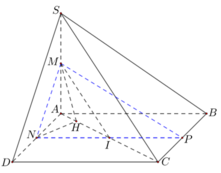
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
A
B
2
,
A
D
2
3
. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi M, N, P lần lượt là trung điểm của các cạnh SA, CD, CB. Tính côsin góc tạo bởi mặt phẳng (MNP) và (SCD). A.
2
435
145
.
B. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = 2 , A D = 2 3 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi M, N, P lần lượt là trung điểm của các cạnh SA, CD, CB. Tính côsin góc tạo bởi mặt phẳng (MNP) và (SCD).
A. 2 435 145 .
B. 11 145 145 .
C. 2 870 145 .
D. 3 145 145 .
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a,
A
D
2
a
, cạnh bên SA vuông góc với đáy và SA 2a. Gọi M, N lần lượt là trung điểm của cạnh SA, CD và
α
là góc giữa đường thẳng MN và mặt phẳng (SBD). Khi đó
sin
α
bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, A D = 2 a , cạnh bên SA vuông góc với đáy và SA = 2a. Gọi M, N lần lượt là trung điểm của cạnh SA, CD và α là góc giữa đường thẳng MN và mặt phẳng (SBD). Khi đó sin α bằng
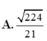
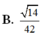
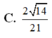
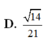
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, cạnh SAa và vuông góc với mặt đáy. Gọi M, N lần lượt là trung điểm các cạnh BC, SD,
α
là góc giữa đường thẳng MN và (SAC). Giá trị tan
α
là A.
6
3
B.
6
2
C.
3...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, cạnh SA=a và vuông góc với mặt đáy. Gọi M, N lần lượt là trung điểm các cạnh BC, SD, α là góc giữa đường thẳng MN và (SAC). Giá trị tan α là
A. 6 3
B. 6 2
C. 3 2
D. 2 3
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, cạnh SAa và vuông góc với mặt đáy. Gọi M, N lần lượt là trung điểm các cạnh BC, SD,
α
là góc giữa đường thẳng MN và (SAC). Giá trị tan
α
là A.
6
3
B.
6
2
C.
3...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, cạnh SA=a và vuông góc với mặt đáy. Gọi M, N lần lượt là trung điểm các cạnh BC, SD, α là góc giữa đường thẳng MN và (SAC). Giá trị tan α là
A. 6 3
B. 6 2
C. 3 2
D. 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,
S
A
⊥
(
A
B
C
D
)
,
S
A
a
6
. Gọi
α
là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định s...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ ( A B C D ) , S A = a 6 . Gọi α là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau?
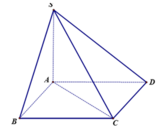
A. α = 30 o
B. cos α = 3 3
C. α = 45 o
D. α = 60 o
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,
S
A
⊥
(
A
B
C
D
)
. Gọi
α
là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau?
Đọc tiếp
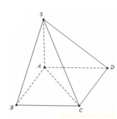
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ ( A B C D ) . Gọi α là góc giữa SC và mp (ABCD). Chọn khẳng định đúng trong các khẳng định sau?
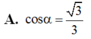
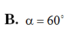
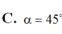
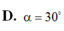
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AB//CD). Gọi I, J lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm tam giác SAB. Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sau đây đúng?
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AB//CD). Gọi I, J lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm tam giác SAB. Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sau đây đúng?
![]()
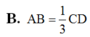
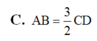
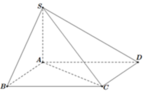
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh ABa, ADa
3
. Cạnh bên SAa
2
và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SB và mặt phẳng (SAC)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh AB=a, AD=a 3 . Cạnh bên SA=a 2 và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SB và mặt phẳng (SAC)
![]()
![]()
![]()
![]()
Cho khối chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và (ABCD) bằng
45
o
. Gọi M, N lần lượt là trung điểm AB, AD. Tính thể tích khối chóp S. CDMN theo a. A.
5
a
3
8
B.
a
3
8...
Đọc tiếp
Cho khối chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45 o . Gọi M, N lần lượt là trung điểm AB, AD. Tính thể tích khối chóp S. CDMN theo a.
A. 5 a 3 8
B. a 3 8
C. 5 a 3 24
D. a 3 3