Đáp án C
Ta có V S . A I C V S . A B C = S I S B = 1 3 ⇒ V S . A I C = 1 3 V S . A B C = 1 3 . 1 3 S A . 1 2 B A . B C
= 1 18 a . B A 2 = 1 18 a . 2 a 2 2 = a 3 9
Đáp án C
Ta có V S . A I C V S . A B C = S I S B = 1 3 ⇒ V S . A I C = 1 3 V S . A B C = 1 3 . 1 3 S A . 1 2 B A . B C
= 1 18 a . B A 2 = 1 18 a . 2 a 2 2 = a 3 9
Cho hình chóp .S ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( A B C ) , B C = a , góc hợp bởi (SBC) và SBC) là 60 0 Mặt phẳng (P) qua A vuông góc với SC cắt SB, SC lần lượt tại D, E. Thể tích khối đa diện ABCED là
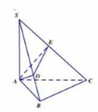
A. a 3 3 6
B. 11 a 3 3 120
C. 11 a 3 3 60
D. 3 a 3 3 40
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB=a. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 45 0 .
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và AB=AC=a, biết tam giác cân SAB cân tại S và nằm trong mặt phẳng vuông góc với (ABC). Mặt phẳng (SAC) hợp với mặt phẳng (ABC) một góc bằng . Thể tích của khối chóp S.ABC bằng
A. a 3 3
B. a 3 4
C. a 3 9
D. a 3 12
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a, cạnh bên SB vuông góc với mặt phẳng A B C , S B = 2 a . Tính thể tích khối chóp S,ABC.
A. a 3 4
B. a 3 3 6
C. 3 a 3 4
D. a 3 3 2
Cho hình chóp S.ABCD có đáy là tam giác đều cạnh a , mặt phẳng (SAB) vuông góc với mặt phẳng (ABC) và tam giác SAB vuông cân tại S . Tính thể tích khối chóp S.ABC theo a
A. a 3 3 12
B. a 3 3 24
C. a 3 3 3
D. a 3 3 4
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở A, cạnh BC=2 3 a. Tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp là a 3 , tính góc giữa SA và mặt phẳng (SBC).
A. π /6
B. π /3
C. π /4
D. arctan 3 2
Cho hình chóp S.ABC có tam giác ABC vuông tại A, BC = 2a, góc ACB = 60 ° . Mặt phẳng (SAB) vuông góc với mặt phẳng (ABC), tam giác SAB cân tại S, tam giác SBC vuông tại S. Thể tích khối chóp S.ABC là:
A. a 3 2
B. a 3 4
C. a 3 8
D. a 3 16
Cho hình chóp S.ABC có đáy là tam giác vuông cận tại B , AB = a . Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60 0 . Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).
A. 8 2 πa 3 3
B. 4 2 πa 3 3
C. 2 2 πa 3 3
D. 2 πa 3 3
Cho hình chóp S.ABCcó đáy ABC là tam giác đều cạnh AB = a(a > 0) Mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Thể tích khối chóp S.ABC là:
A. a 3 3 24
B. a 3 3 8
C. a 3 3 3
D. a 3 3 6