Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi
V
1
là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết
V
1
V
20
27
. Tỉ số
S
M
S
B...
Đọc tiếp
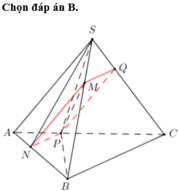
Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi V 1 là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết V 1 V = 20 27 . Tỉ số S M S B bằng:
A. 2 3
B. 1 2
C. 3 4
D. 4 5
Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi
V
1
là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết
V
1
V
20
27
. Tỉ số
S
M
S
B...
Đọc tiếp
Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi V 1 là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết V 1 V = 20 27 . Tỉ số S M S B bằng
A. 2 3
B. 1 2
C. 3 4
D. 4 5
Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của khối chóp tam giác S.ABC sao cho
S
M
M
A
1
2
;
S
N
N
B
2
.
Mặt phẳng
α
đi qua MN và song song với SC chia khối chóp thàng 2 phần. Gọi...
Đọc tiếp
Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của khối chóp tam giác S.ABC sao cho S M M A = 1 2 ; S N N B = 2 . Mặt phẳng α đi qua MN và song song với SC chia khối chóp thàng 2 phần. Gọi V 1 là thể tích của khối đa diện chứa A , V 2 là thể tích của khối đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 4 5
B. V 1 V 2 = 5 4
C. V 1 V 2 = 5 6
D. V 1 V 2 = 6 5
Cho hình chóp S.ABC có đáy vuông cân ở B,
A
C
a
2
;
S
A
⊥
A
B
C
;
S
A
a
. Gọi G là trọng tâm của
∆
S
B
C
, mp
α
đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi V là thể tích của khối đa diện không ch...
Đọc tiếp
Cho hình chóp S.ABC có đáy vuông cân ở B, A C = a 2 ; S A ⊥ A B C ; S A = a . Gọi G là trọng tâm của ∆ S B C , mp α đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S. Tính V.
A. 5 a 3 54
B. 4 a 3 9
C. 2 a 3 9
D. 4 a 3 27
Cho khối chóp S.ABC trên ba cạnh SA,SB,SC lần lượt lấy ba điểm A, B, C sao cho
S
A
1
2
S
A
;
S
B
1
3
S
B
;
S
C
1
4
S
C
,
Gọi V và V lần lượt là thể tích của khối chóp S.ABC và S.ABC Khi đó tỉ số
V
V
là...
Đọc tiếp
Cho khối chóp S.ABC trên ba cạnh SA,SB,SC lần lượt lấy ba điểm A', B', C' sao cho S A ' = 1 2 S A ; S B ' = 1 3 S B ; S C ' = 1 4 S C , Gọi V và V' lần lượt là thể tích của khối chóp S.ABC và S.A'B'C' Khi đó tỉ số V ' V là:
A.12
B. 1 12
C.24
D. 1 24
Cho khối chóp
S
.
A
B
C
, trên ba cạnh
S
A
,
S
B
,
S
C
lần lượt lấy ba điểm
A
,
B
,
C
sao cho
S
A
2
3
A
A...
Đọc tiếp
Cho khối chóp S . A B C , trên ba cạnh S A , S B , S C lần lượt lấy ba điểm A ' , B ' , C ' sao cho S A ' = 2 3 A A ' , S B ' = 1 4 S B , S C ' = 1 2 C C ' . Gọi V và V′ lần lượt là thể tích của các khối chóp S . A B C và S . A ' B ' C ' . Khi đó tỉ số V ' V là
A. 1 30
B. 1 24
C. 1 8
D. 1 8
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm
A
,
B
,
C
sao cho
S
A
1
3
S
A
,
S
B
1
3
S
B
,
S
C
1
3
S
C...
Đọc tiếp
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A ' , B ' , C ' sao cho S A ' = 1 3 S A , S B ' = 1 3 S B , S C ' = 1 3 S C . Gọi V và V' lần lượt là thể tích của các khối chóp S.ABC và S.A'B'C'. Khi đó tỉ số V ' V là
A. 1 6
B. 1 3
C. 1 27
D. 1 9
Cho hình chóp S.ABC, M và N là các điểm thuộc các cạnh SA và SB sao cho MA 2SM, SN 2NB,
α
là mặt phẳng qua MN và song song với SC. Kí hiệu (H1) và (H2) là các khối đa diện có được khi chia khối chóp S.ABC bới mặt phẳng
α
trong đó (
H
1
) chứa điểm S, (
H
2
) chứa điểm A;
V
1
và
V
2...
Đọc tiếp
Cho hình chóp S.ABC, M và N là các điểm thuộc các cạnh SA và SB sao cho MA= 2SM, SN = 2NB, α là mặt phẳng qua MN và song song với SC. Kí hiệu (H1) và (H2) là các khối đa diện có được khi chia khối chóp S.ABC bới mặt phẳng α trong đó ( H 1 ) chứa điểm S, ( H 2 ) chứa điểm A; V 1 và V 2 lần lượt là thể tích của ( H 1 ) và ( H 2 ). Tính tỉ số V 1 V 2
A. 4/3
B. 5/4
C. 3/4
D. 4/5
Cho khối chóp S.ABC có
M
∈
S
A
,
N
∈
S
B
sao cho
M
A
→
−
2
M
S
→
,
N
S
→
−
2
N
B
→...
Đọc tiếp
Cho khối chóp S.ABC có M ∈ S A , N ∈ S B sao cho M A → = − 2 M S → , N S → = − 2 N B → . Mặt phẳng α đi qua hai điểm M, N và song song với SC chia khối chóp thành hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó (số bé chia số lớn).
A. 3/5
B. 4/5
C. 4/9
D. 3/4