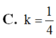Các câu hỏi tương tự
Cho hình chóp S.ABC có SAa, SBb, SCc. Một mặt phẳng (α) đi qua trọng tâm của tam giác ABC, cắt các cạnh SA, SB, SC lần lượt tại A’, B’, C’. Tìm giá trị nhỏ nhất của
1
S
A
2
+
1
S
B
2
+...
Đọc tiếp
Cho hình chóp S.ABC có SA=a, SB=b, SC=c. Một mặt phẳng (α) đi qua trọng tâm của tam giác ABC, cắt các cạnh SA, SB, SC lần lượt tại A’, B’, C’. Tìm giá trị nhỏ nhất của 1 S A ' 2 + 1 S B ' 2 + 1 S C ' 2
A. 3 a 2 + b 2 + c 2 .
B. 2 a 2 + b 2 + c 2 .
C. 2 a 2 + b 2 + c 2 .
D. 9 a 2 + b 2 + c 2 .
Cho hình chóp S.ABC có
S
A
S
B
S
C
a
,
A
S
B
^
B
S
C
^
C
S
A
^
α
. Gọi (b) là mặt phẳng đi qua A và các trung điể...
Đọc tiếp
Cho hình chóp S.ABC có S A = S B = S C = a , A S B ^ = B S C ^ = C S A ^ = α . Gọi (b) là mặt phẳng đi qua A và các trung điểm của SB, SC. Tính diện tích thiết diện S của hình chóp cắt bởi mặt phẳng (b).
A. S = a 2 2 7 cos 2 α − 16 cos α + 9
B. S = a 2 2 7 cos 2 α − 6 cos α + 9
C. S = a 2 8 7 cos 2 α − 6 cos α + 9
D. S = a 2 8 7 cos 2 α − 16 cos α + 9
Cho khối chóp S. ABCD có đáy ABCD là tứ giác lồi, tam giác ABD đều cạnh a, tam giác BCD cân tại C và
B
C
D
^
120
0
,
S
A
⊥
A
B
C
D
và SAa. Mặt phẳng (P) đi qua A và vuông...
Đọc tiếp
Cho khối chóp S. ABCD có đáy ABCD là tứ giác lồi, tam giác ABD đều cạnh a, tam giác BCD cân tại C và B C D ^ = 120 0 , S A ⊥ A B C D và SA=a. Mặt phẳng (P) đi qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại M, N, P. Tính thể tích khối chóp S. AMNP.
A. a 3 3 42
B. 2 a 3 3 21
C. a 3 3 14
D. a 3 3 12
Cho hình chóp đều S.ABC có AB a,
A
S
B
^
30
°
. Lấy các điểm B, C lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác ABC nhỏ nhất. Tính chu vi đó. A. (
3
-1)a B.
3
a C.
a
3
+
...
Đọc tiếp
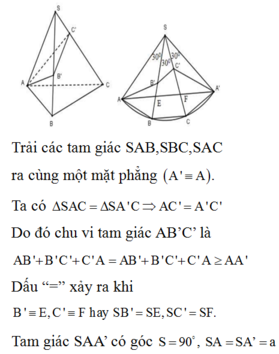
Cho hình chóp đều S.ABC có AB = a, A S B ^ = 30 ° . Lấy các điểm B', C' lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác AB'C' nhỏ nhất. Tính chu vi đó.
A. ( 3 -1)a
B. 3 a
C. a 3 + 1
D. (1+ 3 )a
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA a
2
. Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B, D, C. Thể tích khối chóp S. ABCD là: A. V
2
a
3
3
9
B. V
2
a...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 2 . Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B', D', C'. Thể tích khối chóp S. AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC a/2, SC BC a
2
. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k V/V. A.
k
1
3
B.
k
2
4
C.
k...
Đọc tiếp
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a 2 . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V.

A. k = 1 3
B. k = 2 4
C. k = 4 9
D. k = 2 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC), AB a,
B
C
a
3
, SA a. Một mặt phẳng (α) qua A vuông góc SC tại H và cắt SB tại K. Tính thể tích khối chóp S.AHK theo a A.
V
S
.
A...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC), AB = a, B C = a 3 , SA = a. Một mặt phẳng (α) qua A vuông góc SC tại H và cắt SB tại K. Tính thể tích khối chóp S.AHK theo a
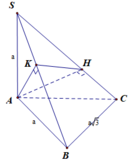
A. V S . A H K = a 3 3 20
B. V S . A H K = a 3 3 30
C. V S . A H K = a 3 3 60
D. V S . A H K = a 3 3 90
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC), AB a, BC
a
3
, SA a. Một mặt phẳng (
α
) qua A vuông góc SC tại H và cắt SB tại K. Tính thể tích khối chóp S.AHK theo a.
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC), AB = a, BC = a 3 , SA = a. Một mặt phẳng ( α ) qua A vuông góc SC tại H và cắt SB tại K. Tính thể tích khối chóp S.AHK theo a.
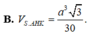
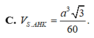

Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC a/2, SC BC a
2
. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính thể tích V của hình chóp S.A’B’C. A.
V
14
54
a
3
B.
V
14
64
a...
Đọc tiếp
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a 2 . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính thể tích V của hình chóp S.A’B’C.
A. V = 14 54 a 3
B. V = 14 64 a 3
C. V = 14 49 a 3
D. V = 4 61 a 3