Các câu hỏi tương tự
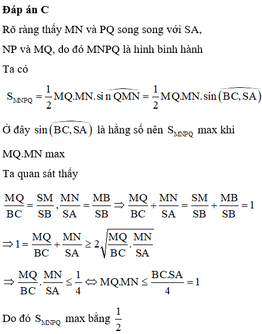
Cho khối chóp S.ABC có SA=AB=BC=2 và M là một điểm thuộc SB. Dựng thiết diện qua M song song với SA, BC cắt AB, AC, SC lần lượt tại N, P, Q. Diện tích thiết diện MNPQ lớn nhất bằng
A. 1
B. 2
C. 1/2
D. 1/4
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x (0xa). Mặt phẳng
(
α
)
qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A.
x
a
4
B.
x
a
3
C.
x
a...
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0<x<a). Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM x
0
x
α
. Mặt phẳng
α
qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất. A.
x
a
4
B.
x...
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x 0 < x < α . Mặt phẳng α qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB 1, AC 2; cạnh bên SA vuông góc với đáy và SA 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho
A
M
x
0
x
1
và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng. A. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = 1, AC = 2; cạnh bên SA vuông góc với đáy và SA = 1. Gọi I là trung điểm của AC. Xét M là điểm thay đổi trên cạnh AB sao cho A M = x 0 < x < 1 và (P) là mặt phẳng đi qua M, song song với SA và IB. Thiết diện của hình chóp với mặt phẳng (P) có diện tích lớn nhất thì giá trị của x bằng.
A. 2 3
B. 3 4
C. 1 3
D. 1 2
Cho hình chóp S.ABC có
S
A
S
B
S
C
3
,
tam giác ABC vuông cân tại B và
A
C
2
2
. Gọi M, N lần lượt là trung điểm của AC và BC. Trên hai cạnh SA, SB lấy các điểm P, Q tương ứng sao cho
S
P
1
,
S
Q
2.
Tính thể tích V của khối tứ diện...
Đọc tiếp
Cho hình chóp S.ABC có S A = S B = S C = 3 , tam giác ABC vuông cân tại B và
A C = 2 2 . Gọi M, N lần lượt là trung điểm của AC và BC. Trên hai cạnh SA, SB lấy các điểm P, Q tương ứng sao cho S P = 1 , S Q = 2. Tính thể tích V của khối tứ diện M N P Q .
A. V = 7 18
B. V = 3 12
C. V = 34 12
D. V = 34 144
Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi
V
1
là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết
V
1
V
20
27
. Tỉ số
S
M
S
B...
Đọc tiếp
Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi V 1 là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết V 1 V = 20 27 . Tỉ số S M S B bằng:
A. 2 3
B. 1 2
C. 3 4
D. 4 5
Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi
V
1
là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết
V
1
V
20
27
. Tỉ số
S
M
S
B...
Đọc tiếp
Cho khối chóp S.ABC có thể tích V, M là một điểm trên cạnh SB. Thiết diện qua M song song với đường thẳng SA và BC chia khối chóp thành hai phần. Gọi V 1 là thể tích phần khối chóp S.ABC chứa cạnh SA. Biết V 1 V = 20 27 . Tỉ số S M S B bằng
A. 2 3
B. 1 2
C. 3 4
D. 4 5
Cho hình chóp S.ABC có đáy là
Δ
A
B
C
vuông cân ở B,
A
C
a
2
,
S
A
a
và
S
A
⊥
A
B
C
. Gọi G là trọng tâm
Δ
S
B
C
, một mặt phẳng
α
đi qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Thể tích khối chóp S.AMN bằng : A. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy là Δ A B C vuông cân ở B, A C = a 2 , S A = a và S A ⊥ A B C . Gọi G là trọng tâm Δ S B C , một mặt phẳng α đi qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Thể tích khối chóp S.AMN bằng :
A. 4 a 3 27
B. 2 a 3 9
C. 4 a 3 9
D. 2 a 3 27
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B,
A
C
a
2
biết SA vuông góc với mặt đáy, SA a. Gọi G là trọng tâm của tam giác SBC,
α
là mặt phẳng đi qua AG và song song với BC cắt SB, SC lần lượt tại M và N. Tính thể tích V của khối đa diện AMNBC. A.
V
4
9
a
3
B.
V...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, A C = a 2 biết SA vuông góc với mặt đáy, SA = a. Gọi G là trọng tâm của tam giác SBC, α là mặt phẳng đi qua AG và song song với BC cắt SB, SC lần lượt tại M và N. Tính thể tích V của khối đa diện AMNBC.
A. V = 4 9 a 3
B. V = 2 27 a 3
C. V = 5 27 a 3
D. V = 5 54 a 3