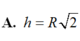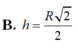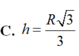Đáp án B
Thể tích của khối cầu
V = 4 3 πR 3 = 36 π
⇔ R 3 = 27 ⇔ R = 3 ( c m )
Đáp án B
Thể tích của khối cầu
V = 4 3 πR 3 = 36 π
⇔ R 3 = 27 ⇔ R = 3 ( c m )
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Cho một mặt cầu có diện tích S, thể tích khối cầu đó là V. Bán kính R của mặt cầu là:
A. R = 4V/S B. R = S/3V
C. R = 3V/S D. R = V/3S
Một con xoay được thiết kế gồm hai khối trụ T 1 , T 2 chồng lên khối nón (N) (Tham khảo mặt cắt ngang qua trục như hình vẽ). Khối trụ T 1 có bán kính đáy r(cm), chiều cao h 1 (cm) . Khối trụ T 2 có bán kính đáy 2r(cm), chiều cao h 2 = 2 h 1 (cm). Khối nón (N) có bán kính đáy r(cm), chiều cao h n = 4 h 1 (cm). Biết rằng thể tích toàn bộ con xoay bằng 31 c m 3 . Thể tích khối nón (N) bằng
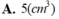
![]()
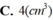
![]()
Bán kính r của khối cầu có thể tích V = 36 π c m 3 là
A. 3 cm
B. 6 cm
C. 4 cm
D. 9 cm
I. Trắc nghiệm ( 6 điểm)
Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.
A. R = 3 V S
B. R = S 3 V
C. R = 4 V S
D. R = V 3 S
Một khối nón có độ dài đường sinh là l=13 cm và bán kính đáy r=5 cm. Khi đó thể tích khối nón là
A. V = 100 π c m 3
B. V = 300 π c m 3
C. V = 325 3 π c m 3
D. V = 20 π c m 3
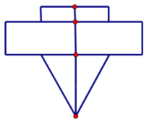
Cho khối cầu tâm I, bán kính R không đổi. Một khối nón có chiều cao h và bán kính đáy r, nội tiếp khối cầu. Tính chiều cao h theo bán kính R sao cho khối nón có thể tích lớn nhất.
![]()
![]()
![]()
![]()
Một khối cầu có thể tích bằng 32 π 3 . Bán kính R của khối cầu đó là
![]()
![]()
![]()
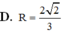
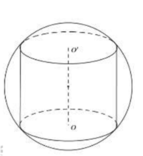
Cho khối cầu (S) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.