Phương pháp:
Sử dụng công thức khai triển của nhị thức Newton:
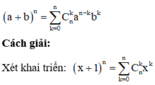
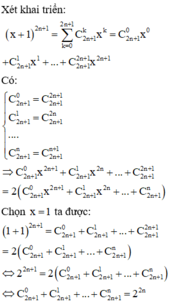
Theo bài ra ta có:

Phương pháp:
Sử dụng công thức khai triển của nhị thức Newton:
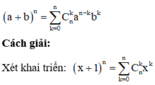
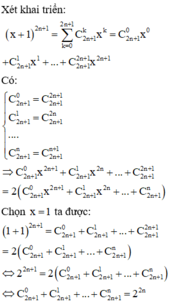
Theo bài ra ta có:

Gọi a là hệ số không chứa x trong khai triển khai triển nhị thức Niu-tơn x 2 − 2 x n = C n 0 x 2 n + C n 1 x 2 n − 1 − 2 x + … + C n n − 1 x 2 − 2 x n − 1 + C n n − 2 x n (n là số nguyên dương).
Biết rằng trong khai triển trên tổng hệ số của ba số hạng đầu bằng 161. Tìm a
A. a = 11520
B. a = 11250
C. a = 12150
D. a = 10125
Biết n là số nguyên dương thỏa mãn C n n - 1 + C n n - 2 = 78 . Số hạng chứa x 4 trong khai triển ( x 2 - 2 x 2 ) n là
A. 126720
B. -25344 x 4
C.-112640
D. 25344 x 4
Biết n là số nguyên dương thỏa mãn C n n - 1 + C n n - 2 = 78 , số hạng chứa x 8 trong khai triển ( x 3 - 2 x ) n là:
A. - 10176 x 8
B. -101376
C. -112640
D. 101376 x 8
Tìm hệ số của x trong khai triển
P x = 1 + n 4 x - 3 n 8 x 3 n - 4 với x > 0. Biết n là số nguyên dương thỏa mãn điều kiện
A n 2 + 3 C n n - 2 - C n + 1 3 = A n + 1 2 - 2 n
A. 28
B. 78
C. 218
D. 80
Xét n là số nguyên dương thỏa mãn điều kiện C n + 4 n + 1 - C n + 3 n = 7 n + 3 . Hệ số của số hạng chứa x 8 trong khai triển 1 x 3 + x 5 n với x > 0, bằng
A. 549
B. 954
C. 945
D. 495
Cho n là số nguyên dương thỏa mãn 5 C n n - 1 - C n 3 = 0 . Tìm hệ số của số hạng chứa x 5 trong khai triển nhị thức Niu-tơn của x 2 2 - 1 x n , x ≢ 0
A. - 35 16 x 5
B. - 35 16
C. - 35 16 x 2
D. 35 16 x 5
Biết n là số nguyên dương thỏa mãn C n n - 1 + C n n - 2 = 78 , số hạng chứa x 8 trong khai triển x 3 - 2 x n là
A. - 101376 x 8
B. -101376
C. -112640
D. - 112640 x 8
Biết n là số nguyên dương thỏa mãn C n n − 1 + C n n − 2 = 78 . Số hạng chứa x 4 trong khai triển x 2 − 2 x n là
A. 126720
B. − 25344 x 4
C. 25344 x 4
D. - 112640
Trong khai triển nhị thức ( x + 1 x ) n hệ số của số hạng thứ 3 lớn hơn hệ số của số hạng thứ 2 là 35. Tìm số hạng không chứa x trong khai triển nói trên.
A. 225
B. 252
C. 522
D. 525