Chọn A
Ta có: 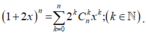
Suy ra: ![]()
Thay ![]()
![]()
vào giả thiết ta có: ![]()
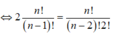
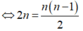
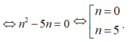
Chọn A
Ta có: 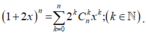
Suy ra: ![]()
Thay ![]()
![]()
vào giả thiết ta có: ![]()
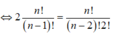
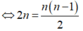
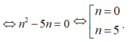
Cho khai triển nhị thức Niuton x 2 + 2 n x n với n n ∈ ℕ , x > 0. Biết rằng số
hạng thứ 2 của khai triển bằng 98 và n thỏa mãn A n 2 + 6 C n 3 = 36 n Trong các giá trị x sau, giá trị nào thỏa mãn?
A. 3
B. 4
C. 1
D. 2
Tìm hệ số của x trong khai triển P x = 1 + n 4 x - 3 n 8 x 3 n - 4 với x > 0 . Biết n là số nguyên dương thỏa mãn điều kiện A n 2 + 3 C n n - 2 - C n + 1 3 = A n + 1 2 - 2 n .
A. 28
B. 78
C. 218
D. 80
Tìm số hạng chứa x5 trong khai triển \(\left(x-\dfrac{2}{x}\right)^{n^{ }}\) , biết n là số tự nhiên thỏa mãn \(C^3_n=\dfrac{4}{3}n+2C^2_n\)
A.144 B.134 C.115 D.141
Cho số nguyên dương n thỏa mãn điều kiện: 720 C 7 7 + C 8 7 + C 9 7 + . . . + C n 7 = 1 4032 A n + 1 10 . Hệ số của x 7 trong khai triển x - 1 x 2 n ( x ≠ 0 ) bằng:
A. -120
B. -560
C. 120
D. 560
Cho n là số nguyên dương thỏa mãn C n 2 - C n 1 = 44 Số hạng không chứa x trong khai triển của biểu thức ( x x + 1 x 4 ) n , với x > 0 bằng:
A.165.
B.485.
C.238.
D.525.
Cho n là số nguyên dương thỏa mãn 5 C n n - 1 - C n 3 = 0 . Tìm hệ số của số hạng chứa x 5 trong khai triển nhị thức Niu-tơn của x 2 2 - 1 x n , x ≠ 0
A. - 35 16 x 5
B. - 35 16
C. - 35 2 x 2
D. 35 16 x 5
tồn tại hay không số nguyên dương m,n,p thỏa mãn đồng thời các điều kiện (m+n,mn-1)=1, (m-n; mn+1)=1 và \(\text{(m+n)^2+(mn-1)^2=p^2}\)?. (Trong đó (a,b) là ước chung lớn nhất của 2 số nguyên dương a và b)
Hãy xác định giá trị của x trên đoạn [- π ; 3π/2] để hàm số y = tan x:
a. Nhận giá trị bằng 0
b. Nhận giá trị bằng 1
c. Nhận giá trị dương
d. Nhận giá trị âm
Cho f(x)=1/3(m-1)x³-mx²+(m+2)x-5. Tìm m để a)f'(x) lớn hơn hoặc bằng 0 với mọi x b)f'(x) nhỏ hơn hoặc bằng 0 với mọi x c)f'(x)=0 có 2 nghiệm cùng âm d)f'(x)=0 có nghiệm thỏa mãn x1+2x2=1