Các câu hỏi tương tự
Với k là số nguyên dương bất kỳ, xét các mệnh đề sau: 1.
lim
x
→
+
∞
1
x
k
+
∞
2
.
lim
x
→
-
∞
1
x
k...
Đọc tiếp
Với k là số nguyên dương bất kỳ, xét các mệnh đề sau:
1. lim x → + ∞ 1 x k = + ∞
2 . lim x → - ∞ 1 x k = 0 3 . lim x → + ∞ x k = + ∞ 4 . lim x → - ∞ x k = + ∞ n ế u k c h ẵ n 5 . lim x → - ∞ x k = 0 n ế u k l ẻ
Số mệnh đề đúng là:
A.2
B.3
C.4
D.5
Xét các mệnh đề sau (I).
l
i
m
n
k
+
∞
với k là số nguyên dương tùy ý. (II).
lim
x
→
∞
1
x
k
0
với k là số nguyên dương tùy ý. (III).
lim
x
→
-...
Đọc tiếp
Xét các mệnh đề sau
(I). l i m n k = + ∞ với k là số nguyên dương tùy ý.
(II). lim x → ∞ 1 x k = 0 với k là số nguyên dương tùy ý.
(III). lim x → - ∞ x k = + ∞ với k là số nguyên dương tùy ý.
Trong 3 mệnh đề trên thì
A. Cả (I), (II), (III) đều đúng.
B. Chỉ (I) đúng
C. Chỉ (I),(II) đúng
D. Chỉ (III) đúng
Cho k, n, 1
≤
k
≤
n là các số nguyên dương bất kì. Mệnh đề nào sau đây sai?
A
.
C
n
k
A
n
k
k
!
B
.
C
n
k
A...
Đọc tiếp
Cho k, n, 1 ≤ k ≤ n là các số nguyên dương bất kì. Mệnh đề nào sau đây sai?
A . C n k = A n k k !
B . C n k = A n k ( n - k ) !
C . C n k = n ! k ! ( n - k ) !
D . A n k = n ! ( n - k ) !
Cho k,n
k
n
là các số nguyên dương. Mệnh đề nào sau đây sai ?
Đọc tiếp
Cho k,n k < n là các số nguyên dương. Mệnh đề nào sau đây sai ?
![]()
![]()
![]()
![]()
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:A(n) : “nếu a và b là những số nguyên dương mà max{a,b} n thì a b”Chứng minh :Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} 1 thì a b”Mệnh đề A(1) đúng vì max{a,b} 1 và a,b là những số nguyên dương thì a b 1.Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1Bước 3: xét max{a,b} k+1 ⇒max{a-1,b-1} k+ 1-1 kDo a(k) là mệnh đề đúng nên a- 1 b-1 ⇒ a b⇒...
Đọc tiếp
Hãy xem trong lời giải của bài toán sau đây có bước nào bị sai?
Bài toán: chứng minh rằng với mọi số nguyên dương n, mệnh đề sau đây đúng:
A(n) : “nếu a và b là những số nguyên dương mà max{a,b} = n thì a = b”
Chứng minh :
Bước 1: A(1):”nếu a,b là những số nguyên dương mà max{a,b} = 1 thì a = b”
Mệnh đề A(1) đúng vì max{a,b} = 1 và a,b là những số nguyên dương thì a= b =1.
Bước 2: giả sử A(k) là mệnh đề đúng vơi k≥1
Bước 3: xét max{a,b} = k+1 ⇒max{a-1,b-1} = k+ 1-1 = k
Do a(k) là mệnh đề đúng nên a- 1= b-1 ⇒ a= b⇒ A(k+1) đúng.
Vậy A(n) đúng với mọi n ∈N*
A. Bước 1
B. Bước 2
C. Bước 3
D. Không có bước nào sai
Cho số nguyên dương n và số nguyên dương k với 0 ≤ k ≤ n. Mệnh đề nào sau đây đúng?
A
.
C
n
k
C
n
n
-
k
B
.
C
n
k
C
n
-...
Đọc tiếp
Cho số nguyên dương n và số nguyên dương k với 0 ≤ k ≤ n. Mệnh đề nào sau đây đúng?
A . C n k = C n n - k
B . C n k = C n - k n
C . C n k = C n k + 1
D . C n k = C n + 1 n - k
Cho k, n(k n) là các số nguyên dương, mệnh đề nào dưới đây sai?
A
.
C
n
k
n
!
k
!
(
n
-
k
)
!
B
.
C
n
k...
Đọc tiếp
Cho k, n(k < n) là các số nguyên dương, mệnh đề nào dưới đây sai?
A . C n k = n ! k ! ( n - k ) !
B . C n k = C n n - k
C . A n k = n ! . C n k
D . A n k = k ! C n k
Cho
k
,
n
k
n
là các số nguyên dương. Mệnh đề nào sau đây sai?
Đọc tiếp
Cho k , n k < n là các số nguyên dương. Mệnh đề nào sau đây sai?
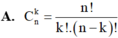
![]()
![]()
![]()
Với k, n là hai số nguyên dương tùy ý thỏa mãn k ≤ n-1, mệnh đề nào dưới đây sai?
A
.
A
n
k
C
n
k
B
.
A
n
k
n
!
(
n
-...
Đọc tiếp
Với k, n là hai số nguyên dương tùy ý thỏa mãn k ≤ n-1, mệnh đề nào dưới đây sai?
A . A n k < C n k
B . A n k = n ! ( n - k ) !
C . C n k + C n k + 1 = C n + 1 k + 1
D . C n k = C n n - k




