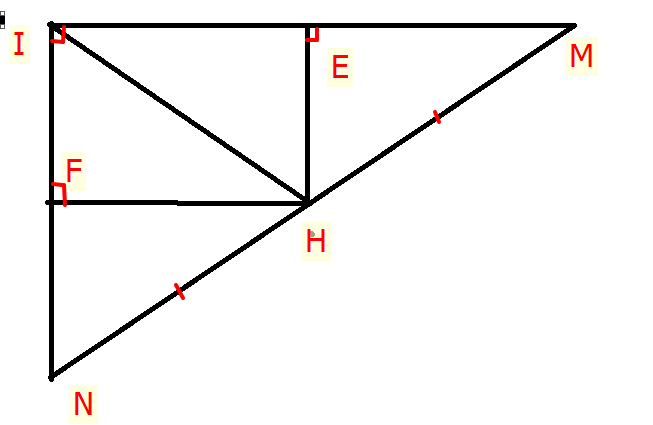
a) Xét ΔNIM vuông tại I có : IH là đường trung tuyến
→ IH = \(\dfrac{1}{2}MN=\dfrac{1}{2}.12=6\)cm
b) Xét tứ giác IEFH có : \(\widehat{EIF}=\widehat{IFH\:}=\widehat{IEH}=90\)
→ IEHF là hình chữ nhật ( DHNB hình chữ nhật )
Bài 4: Cho ∆ABC vuông tại A ( AB < AC ) , đường cao AH (H \in BC) . Kẻ HD vuông góc với AB tại D và HE vuông góc với AC tại E.
a) Tứ giác ADHE là hình gì? Vì sao?
b) Lấy điểm F sao cho E là trung điểm HF. Chứng minh: Tứ giác ADEF là hình bình hành.
c) Gọi M là trung điểm BC. Chứng minh: AM vuông góc với AF.
Bài 1 : Cho tam giác ABC vuông tại A ( AB < AC ) . Gọi I là trung điểm của BC . Qua I vẽ IM vuông góc AB tại M và IN vuông góc AC tại N .
a ) Tứ giác AMIN là hình gì ? Vì sao?
b ) Gọi D là điểm đối xứng của I qua N . Chứng minh : ADCI là hình thoi .
c ) Đường thẳng BC cắt DC tại K . Chứng minh : \(\frac{DC}{DK}\)= \(\frac{1}{3}\)
Bài 2 : Cho tam giác MNK vuông góc tại M ( MN< MK ) . Gọi H là trung điểm của NK . Qua H vẽ HD vuông góc với MN , HE vuông góc với NK tại E .
a ) Tứ giác MDHE là hình gì ? Vì sao ?
b ) Gọi P là diểm đối xứng với H qua E . Chứng minh : MPKH là hình thoi =
c ) Đường thẳng NF cắt PK tại F . Chứng minh \(\frac{PF}{PK}\)= \(\frac{1}{3}\)
Cho tam giác ABC vuông tại A ; AH vuông góc với BC tại H . Điểm E đối xứng với H qua AB , điểm F đối xứng với H qua AC . AB cắt EH tại M , AC cắt HF tại N
a. Tứ giác AMHN là hình gì ? Vì sao ?
b. Chứng minh E đối xứng với F qua A
c. Kẻ trung tuyến AI của tam giác ABC .Chứng minh AI vuông góc MN
Cho tam giác ABC có đường cao AE, BD cắt nhau tại H. từ E kẻ EK vuông góc AC, HK cắt ED tại I. từ I kẻ IM vuông góc AC. N là giao điểm của Im và AE. CM
a, I là trung điểm của MN
b, 1/HD + 1/EK = 2/MN
Cho tam giác ABC vuông tại A ,đường cao AH. D,E lần lượt là trung điểm của AB và AC. a) tứ giác AHDE, DECH là hình gì? vì sao. F đối xứng với H qua E. Tứ giác AHCF là hình gì?vì sao. c) DF cắt AE tại M, DC cắt HE tại N Chứng minh MN vuông góc với DE
Cho △ABC vuông tại A, AH ⊥ BC tại H; AB=8cm; AC=15cm.
a) Tính BH, AH.
b) Từ H kẻ HE ⊥ AB tại E, HF ⊥ AC tại F. Tính EF.
c) Chứng minh AE * AB = AF * AC
d) Qua A kẻ đường vuông góc với EF tại I ,cắt BC tại M. Chứng minh M là trung điểm của BC.
e) Biết diện tích △ABC gấp đôi diện tích tứ giác AEHF. Chứng minh △ABC vuông cân.
) Cho ABC vuông tại A, M là trung điểm của BC. Biết BC = 10 (cm)
Từ M kẻ ME vuông góc AB tại E (E e AB) và MF vuông góc AC tại F (F e AC)
a) Vẽ hình, ghi giả thiết kết luận.
b) Tính AM.
c) Chứng minh AEMF là hình chữ nhật
tam giác abc cân tại A. D thuộc đoạn thẳng BC, E thuộc tia đối của tia CB sao cho BD = CE. Các đường thăngr vuông góc Bc kẻ từ D và E cắt AB, AC ở M,N. I là gia của MN và BE.
a) Biết AB < BC. Chứng minh A> 60.
b) CM IM = IN.
c) CM đường thẳng vuông góc MN tại I luôn đi qua 1 điểm cố định khi D di đôngj trên BC
Cho tam giác ABC vuông cân tại A , gọi MN lần lượt là trung điểm của AB và AC, kẻ NH vuông góc với CM, HE vuông góc AB tại E, từ A kẻ AK vuông góc CM, AQ vuông góc HN. Chứng minh rằng AKHQ là hình vuông.
