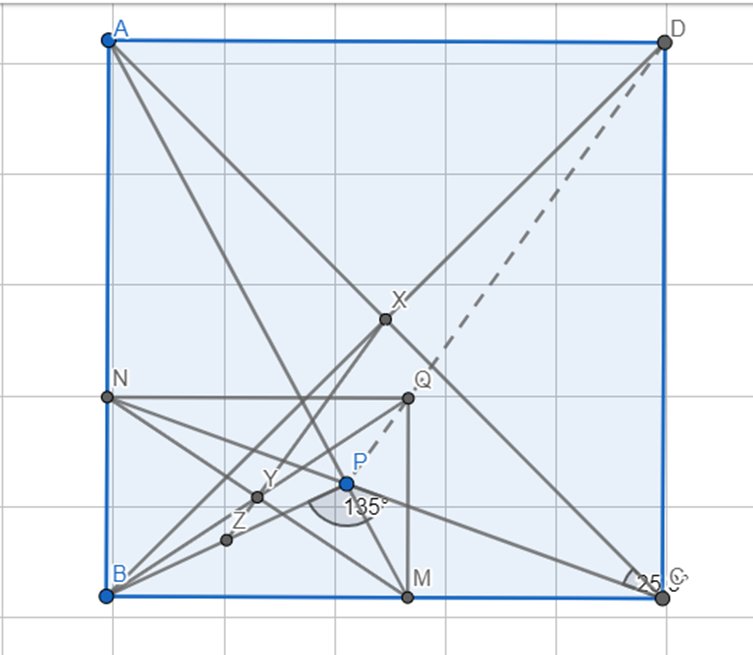
Cho hình vuông ABCD và điểm P nằm trong tam giác ABC.
a) Giả sử \(\widehat{BPC}=135^{\circ}\). Chứng minh rằng \(AP^2=CP^2+2BP^2\).
b) Các đường thẳng AP và CP cắt các cạnh BC và AB tương ứng tại các điểm M và N. Gọi Q là điểm đối xứng với B qua trung điểm của đoạn MN. Chứng minh rằng khi P thay đổi trong tam giác ABC, đường thẳng PQ luôn đi qua D.
a) Cách 1: (dùng kiến thức lớp 8) Dựng tam giác BPF vuông cân tại B (F,P khác phía so với BC) (ở THPT thì có cách nói khác là xét phép dời hình S tâm B biến A-->C, dựng điểm F sao cho S: P--->F).
Gợi ý: Chứng minh △BFC=△BPA, từ đó dùng định lí Pythagoras để chứng minh đẳng thức trên.
Cách 2: (cách này hơi tà đạo chút :) , mà thường lên lớp cao thì ta hay nghĩ đến cách này nhiều hơn).
Dễ dàng chứng minh \(\widehat{PBC}=\widehat{ACP}\).
Áp dụng định lí cos trong △BPC, ta có:
\(BC^2=BP^2+CP^2-2\cos135^0.BP.CP=BP^2+CP^2+\sqrt{2}BP.CP\)
\(\cos\widehat{CBP}=\dfrac{BP^2+BC^2-PC^2}{2BP.BC}\)
Áp dụng định lí cos trong △APC, ta có:
\(\)\(AP^2=AC^2+PC^2-2AC.PC.\cos\widehat{ACP}\)
\(=AC^2+PC^2-AC.PC.\dfrac{BP^2+BC^2-PC^2}{BP.BC}\)
\(=AC^2+PC^2-\sqrt{2}PC.\dfrac{BP^2+BC^2-PC^2}{BP}\)
\(=AC^2+PC^2-\sqrt{2}PC.\dfrac{2BP^2+\sqrt{2}BP.CP}{BP}\)
\(=AC^2+PC^2-\sqrt{2}PC.\left(2BP+\sqrt{2}CP\right)\)
\(=AC^2-PC^2-2\sqrt{2}BP.CP\)
\(=2\left(BP^2+CP^2+\sqrt{2}BP.CP\right)-CP^2-2\sqrt{2}BP.CP=2BP^2+CP^2\left(đpcm\right)\)
b) Đường thẳng Gauss: Cho tứ giác toàn phần ABCD.EFG (nghĩa là cho tứ giác ABCD, AD cắt BC tại E, AB cắt CD tại F, AC cắt BD tại G). Khi đó:
i) Trung điểm của AC,BD,EF thẳng hàng.
ii) Trung điểm của AD,BC,FG thẳng hàng.
iii) Trung điểm của AB,CD,EG thẳng hàng.
(chứng minh bằng cách áp dụng định lí Menelaus, tham khảo cách giải trên mạng).
Quay trở lại bài toán, dễ thấy BMQN là hình chữ nhật. Gọi X,Y lần lượt là tâm của hình vuông ABCD và hình chữ nhật BMQN. Gọi Z là trung điểm BP.
Xét tứ giác toàn phần ACMN.BP (AN cắt CM tại B, AM cắt CN tại P), ta có:
X là trung điểm AC, Y là trung điểm MN, Z là trung điểm BP.
=>X,Y,Z nằm trên đường thẳng Gauss của tứ giác toàn phần ACMN.BP.
Mặt khác: XY//QP (XY là đường trung bình của tam giác BPQ), XZ//PD (XZ là đường trung bình của tam giác BPD) =>P,Q,D thẳng hàng.
=>đpcm.